
 Biometria
- EDAP
Biometria
- EDAPPara visualizar corretamente configurar a tela para 1024 x 768 pixels

 Biometria
- EDAP
Biometria
- EDAPHá vários
tipos
de média (aritmética - simples ou ponderada,
geométrica,
harmônica, quadrática, cúbica,
biquadrática).
A mais usada é a
média
aritmética simples ou, simplesmente,
média, que é obtida
dividindo-se a
soma das
observações
pelo número delas. É um quociente geralmente
representado
pela letra M ou pelo símbolo  (lê-se "x barra").
(lê-se "x barra").
 = (x1
+ x2
+ x3 + x4
+...+
xn) / N =
= (x1
+ x2
+ x3 + x4
+...+
xn) / N = 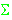 x
/ N
x
/ N
Supondo os seguintes
dados,
já ordenados:
| 4 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 |
| 9 | 9 | 9 | 9 | 9 | 10 | 10 | 10 | 10 | 11 |
| 12 | 12 | 12 | 12 | 12 | 13 | 13 | 13 | 13 | 14 |
| 14 | 15 | 15 | 15 | 15 | 15 | 16 | 17 | 18 | 19 |
| 19 | 19 | 20 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
 =
= 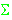 / N = 664 / 50 = 13,28
/ N = 664 / 50 = 13,28 refere-se à média da
amostra (com n elementos) e
deve
ser distinguida da média da
população,
refere-se à média da
amostra (com n elementos) e
deve
ser distinguida da média da
população,  (com N elementos). (topo)
(com N elementos). (topo) =
= 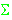 fx
/ n
fx
/ n| x |
f | fx |
| 4 | 1 | 4 |
| 5 | 1 | 5 |
| 6 | 3 | 18 |
| 7 | 3 | 21 |
| 8 | 2 | 16 |
| 9 | 5 | 45 |
| 10 | 4 | 40 |
| 11 | 1 | 11 |
| 12 | 5, sub total: 25 | 60 |
| 13 | 4 | 52 |
| 14 | 2 | 28 |
| 15 | 5 | 75 |
| 16 | 1 | 16 |
| 17 | 1 | 17 |
| 18 | 1 | 18 |
| 19 | 3 | 57 |
| 20 | 2 | 40 |
| 21 | 1 | 21 |
| 22 | 1 | 22 |
| 23 | 1 | 23 |
| 24 | 1 | 24 |
| 25 | 1 | 25 |
| 26 | 1 | 26 |
| Totais | 50 | 664 |
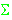 f
= N f
= N |
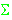 fx fx |
|
| Média: | 664/50 | 13,28 |
A mediana ocupa a posição central de uma
série de dados ordenados.
![]() é o próprio valor
central se a houver um número ímpar de valores na série ou
é o próprio valor
central se a houver um número ímpar de valores na série ou
![]() é
a média aritmética dos dois valores
centrais quando o número de valores da sequência for par.
é
a média aritmética dos dois valores
centrais quando o número de valores da sequência for par.
É absolutamente necessário que os
valores estejam dispostos em
ordem
(crescente ou decrescente) de magnitude. Ou seja, a mediana divide os
dados: 50% dos valores
estão
abaixo
e 50% estão acima da mediana.
Portanto, mediana é o valor
que divide uma série ordenada de modo que pelo menos a
metade das observações sejam iguais ou maiores do
que ela, e que haja pelo menos outra metade de
observações maiores do que ela.
Chama-se de EMd o elemento mediano,
aquele que indica a posição da mediana.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mediana em amostras com até 25 classes com dados classificados Copie a planilha comprimida em formato xls ou como ods |
| Posição | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Total | Média | Mediana |
| A | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 280 | 40 | 40 |
| B | 10 | 20 | 30 | 40 | 50 | 60 | 350 | 360 | 80 | 40 |
É o valor amostral
que tem a maior frequência, ou seja, é o
encontrado
em maior número de vezes, portanto, é a
observação
mais "provável" da distribuição dos
dados. É representada pela
notação Mo e
também
é chamada de "Modo".
Portanto, numa amostra a moda pode não existir. E uma distribuição em que não há elementos repetidos é dita amodal.
Também deve-se considerar que a moda pode
não ser única. Se
dois valores aparecem em igual quantidade de vezes a
distribuição é dita bimodal. Para
três
valores, trimodal, e assim, sucessivamente.
Importante é notar
que se existe apenas uma moda em uma amostra,
há apenas
um grupo de indivíduos com suas
variações, ou
seja,
a amostra é homogênea.
Mas, se houver duas ou mais modas, há grupos diferentes dentro daquela amostra. Diz-se, então, que a amostra é heterogênea. (topo)
Verifica-se qual
é a classe que tem a maior frequência.
Essa classe se
constitui
na moda.
Se os dados estão
agrupados a moda é o ponto médio da classe que
tem a
maior
frequência.
Note-se que uma amostra
pode ter uma moda ou mais (diz-se que a curva é unimodal,
bimodal,
trimodal...)
![]() Processo
empírico
Processo
empírico
Em
distribuições
moderadamente assimétricas pode ser usada a
fórmula de
Pearson,
sendo que:
Como a média
= 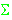 x
/ N = 664 / 50 = 13,28.
x
/ N = 664 / 50 = 13,28.
Portanto, Mo = 3 . 13,25
- 2 . 13,28 = 39,75 - 26,56 = 13,19
![]() Processo
gráfico
Processo
gráfico
Usa-se o histograma gerado
pelos dados, passando-se dois segmentos de reta entre o
vértice
esquerdo da maior coluna e o vértice direito da coluna
seguinte
e entre o vértice direito da maior coluna e o
vértice
esquerdo
da coluna anterior. No ponto onde as retas se cruzam
traça-se
uma
perpendicular à abcissa e o valor encontrado no eixo
dos X
é
a moda. (topo)

Para estudar a variação há várias medidas já definidas. Dentre elas destacam-se a variância e o desvio padrão. (topo)
A variância, representada por s2, e é definida como o "desvio quadrático médio da média".
Note-se que como a variância mede os
desvios em relação à
média
(ou seja, a diferença entre cada dado e a
média) e avalia o grau de dispersão
de
um conjunto de dados.
Considere 3 amostras, A, B e C, com médias
iguais, em que o comprimento de um órgão (em mm)
foi anotado.
| amostra | soma | média | ||||||||||
| A | 160 | 162 | 165 | 168 | 172 | 175 | 1002 | 167 | ||||
| B | 160 | 161 | 162 | 168 | 170 | 173 | 175 | 1169 | 167 | |||
| C | 160 | 162 | 163 | 164 | 165 | 167 | 170 | 171 | 173 | 175 | 1670 | 167 |
 )
e as suas
somas.
)
e as suas
somas.  ),
porque a sua soma em cada amostra
é sempre igual a
zero.
),
porque a sua soma em cada amostra
é sempre igual a
zero.
 )2
e as suas somas:
)2
e as suas somas:
|
A |
desvio |
desvio2 |
B |
desvio |
desvio2 |
C |
desvio |
desvio2 |
|
|
(x- |
(x- |
|
(x- |
(x- |
|
(x- |
(x- |
|
160 |
-7 |
49 |
160 |
-7 |
49 |
160 |
-7 |
49 |
|
162 |
-5 |
25 |
161 |
-6 |
36 |
162 |
-5 |
25 |
|
165 |
-2 |
4 |
162 |
-5 |
25 |
163 |
-4 |
16 |
|
168 |
1 |
1 |
168 |
1 |
1 |
164 |
-3 |
9 |
|
172 |
5 |
25 |
170 |
3 |
9 |
165 |
-2 |
4 |
|
175 |
8 |
64 |
173 |
6 |
36 |
167 |
0 |
0 |
|
|
|
|
175 |
8 |
64 |
170 |
3 |
9 |
|
|
|
|
|
|
|
171 |
4 |
16 |
|
|
|
|
|
|
|
173 |
6 |
36 |
|
|
|
|
|
|
|
175 |
8 |
64 |
|
1002 |
0 |
168 |
1169 |
0 |
220 |
1670 |
0 |
228 |
 )2 é
maior no grupo C,
pois é o que possui maior número
de dados.
)2 é
maior no grupo C,
pois é o que possui maior número
de dados. , a
variância pode ser determinada por:
, a
variância pode ser determinada por: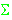 (
xi -
(
xi -  )2
/ (N - 1)
)2
/ (N - 1) 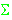 (xi2)
- N
(xi2)
- N  2
/
(N - 1)
2
/
(N - 1) 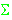 x2
- [(
x2
- [(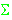 x)2
/
N] / (N - 1)
x)2
/
N] / (N - 1)
Exemplo:
Apenas como exemplo,
suponha que duas amostras apresentaram os seguintes valores de largura
de um órgão, em cm:
A = 8, 10, 12, 14
e 16
B = 4, 8, 12, 16 e 20
Quando se tem todos os dados individuais, ainda sem nenhum tratamento, portanto sem agrupamento em classes, pode-se obter o quadrado dos valores individuais e das duas somatórias.
Exemplo:
Considere 2 amostras, A e B, com 5 dados cada:
| Amostras |
|
|
|||
| x | x2 | x | x2 | ||
| 8 | 64 | 4 | 16 | ||
| 10 | 100 | 8 | 64 | ||
| 12 | 144 | 12 | 144 | ||
| 14 | 196 | 16 | 256 | ||
| 16 | 256 | 20 | 400 | ||
| Total | 60 | 760 | 60 | 880 | |
Variância A
= s2A
= 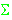 x2
- [(
x2
- [(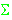 x)2
/
N] / (N - 1) = [760 - (602 / 5)] / 4 =
x)2
/
N] / (N - 1) = [760 - (602 / 5)] / 4 =
= (760 - 720) / 4 = 10
Variância B = s2B
= 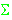 x2
- [(
x2
- [( 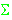 x)2/
N] / (N - 1)
x)2/
N] / (N - 1)
= [880 - (602 / 5)] / 4 = (880 - 720)
/ 4 = 40
Notar que na amostra A os indivíduos estão mais concentrados, distribuindo-se entre o valor mínimo = 8 e o máximo = 16
E, na amostra B estão mais dispersos (distribuindo-se ente 4 e 20).
Assim, na amostra A
a variância ( s2A
= 10) é menor que a da B ( s2B
= 40).
O desvio padrão é obtido simplesmente encontrando-se a raiz quadrada do valor obtido para a variância. É representado por s.
Utilizando os dados do exemplo anterior:
sA =
raiz s2 A =
raiz
10 = 3,16
sB =
raiz s2 B =
raiz
40 = 6,32
Como calcular a variância e o desvio
padrão se não tivermos todos
os dados individuais, ou seja, quando a mostra está dividida
em classes?
Por exemplo, supondo que na literatura
tivéssemos obtido os dados sobre as
frequências dos
intervalos
de classes apresentados para a característica idade:
| Idade |
|
Como
seria possível calcular, a partir apenas desses dados: a.
média
|
| 4 a 7 |
|
|
| 8 a 11 |
|
|
| 12 a 15 |
|
|
| 16 a 19 |
|
|
| 20 a 23 |
|
|
| 24 a 27 |
|
|
Limites
|
Centro
x
|
f
|
fx
|
x2
|
fx2
|
|
4
a 7
|
5,5
|
0
|
0,00
|
30,25
|
0,00
|
|
8
a 11
|
9,5
|
2
|
19,00
|
90,25
|
180,50
|
|
12
a 15
|
13,5
|
1
|
13,50
|
182,25
|
182,25
|
|
16
a 19
|
17,5
|
3
|
52,50
|
306,25
|
918,75
|
|
20
a 23
|
21,5
|
8
|
172,00
|
462,25
|
3698,00
|
|
24
a 27
|
25,5
|
11
|
280,50
|
650,25
|
7152,75
|
|
Total
|
25
|
537,50
|
1721,50
|
12132,25
|
 |
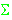 fx
/ n = fx
/ n = |
537,50 / 25 = 21,50 |
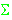 fx2
- [( fx2
- [(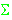 fx)2
/ N]} / (N - 1) = fx)2
/ N]} / (N - 1) = |
[12132,25 - (537,502 / 25)] / 24 = 24,00 | |
| raiz s2 = | raiz 24,00 = 4,8990 |
|
Média, Variância e Desvio Padrão em amostras com até 25 classes com dados classificados Copie a planilha comprimida em formato xls ou em ods |

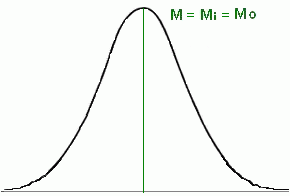 |
Simétrica
-
Tem um só "pico" e apresenta o máximo de
frequência
no centro, diminuindo gradativamente em ambos os lados, até
atingir
valores extremos da escala.
|
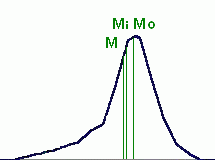 |
Assimétrica
Negativa - Tem um só "pico". A moda apresenta-se
no
máximo
de frequência, sendo maior que a mediana e a
média. Nesse caso, M < Mi < Mo, ou seja a moda é o maior valor dos 3 promédios. |
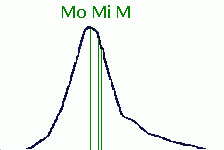 |
Assimétrica
Positiva - Tem um só "pico". A moda apresenta-se
no
máximo
de frequência, sendo menor que a mediana e a
média. Nesse caso, Mo < Mi < M, ou seja a média é o maior valor dos 3 promédios. |
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
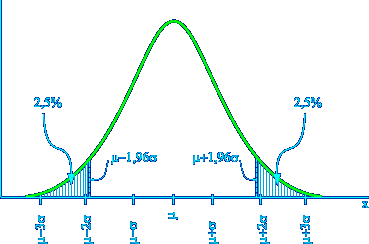 |
||
| População | Amostra | Probabilidade | |
 ±
1s ±
1s |
68,26 % | ||
 ±
2s ±
2s |
95,44 % | ||
 ±
3s ±
3s |
99,74 % | ||
(Se desejar saber como esses valores de probabilidade foram obtidos, clicar aqui).
Importante é notar que ao estudar uma
variável com
distribuição normal em duas ou mais amostras em
geral é necessário saber se uma
amostra difere
significativamente das outras, ou seja, se elas podem ser consideradas
como extraídas da mesma população.
Como a distribuição normal é determinada pela
média e desvio padrão (ou variância)
é óbvio que se as médias e variâncias
de 2 ou +
amostras não diferirem significativamente pode-se aceitar
que
elas foram extraídas da mesma
população. (topo)
As
= ( - Mo) / s
- Mo) / s
Entretanto, a assimetria pode dar-se na cauda esquerda ou na direita da curva de distribuição de frequências, pois, se
 > Mi > Mo
> Mi > Mo
Exemplo:
Usando os dados numéricos anteriores e sabendo-se que o desvio padrão é 5,58, calcule a simetria
As = (13,28 -13,19) /
5,58
= 0,0161
(topo)
|
Copie
esse texto em formato
pdf Depois, clique em"Salvar destino como" (ou algo semelhante ) Escolha o local onde salvar e clique em OK. |
|
Este "site", destinado prioritariamente
aos alunos de Fátima Conti,
está disponível sob FDL (Free
Documentation Licence),
pretende auxiliar quem se interessa por Bioestatística,
estando em permanente
construção.
Sugestões e
comentários
são bem vindos.
Se desejar colaborar
clique
aqui.
Agradeço
antecipadamente.

Deseja enviar essa página?
Se você usa um
programa
de correio eletrônico devidamente configurado para
um e-mail
pop3, clique em "Enviar página" (abaixo) para
abrir o programa.
Preencha o endereço
do destinatário da mensagem.
E pode acrescentar o que quiser.
(Se não der certo,
clique aqui
para saber mais).

Se você usa webmail
copie o endereço abaixo
http://www.cultura.ufpa.br/dicas/biome/bioamos.htm
Acesse a página do seu provedor. Abra uma nova mensagem.
Cole o endereço no campo de texto.
Preencha o endereço do destinatário.
E também pode acrescentar o que quiser.
Última
alteração: 24 mar 2011