
 Biometria
BiometriaPara visualizar corretamente configurar a tela para 1024 x 768 pixels

 Biometria
Biometria| y
= a + bx em que |
|
|
y
=
|
variável dependente |
|
x
=
|
variável independente |
|
a
=
|
constante = intercepto (ponto em que a reta corta o eixo dos y) |
|
b
=
|
constante = coeficiente de regressão |
a = 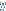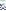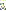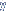 – b.
– b.
Ressalte-se que necessariamente o ponto determinado pela
média
das variáveis está contido na reta.
|
|
|
|
|
|
|
Em que: |
|
|
|
total de larguras = 520 |
|
|
|
total de idades = 36 |
|
|
|
|
|
|
|
média de larguras = 65 |
|
|
|
média de idades = 4,5 |
|
|
|
|
|
|
|
Supondo a = 20 e b = 10 |
y = 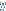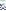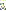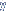 + b.(x -
+ b.(x -  )
)
Portanto,
para a idade x = 1 ano,
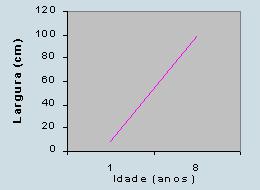
largura: y = 65 + 10 (1 - 4,5) = 30
para a idade x = 8 anos, largura: y = 65 + 10 (8 - 4,5) = 100
E chega-se ao seguinte gráfico:
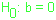 ,
ou seja, H.
Nula:
a reta de regressão em y é
paralela ao eixo dos x
,
ou seja, H.
Nula:
a reta de regressão em y é
paralela ao eixo dos x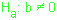 ,
isto é, H.
Alternativa:
a reta de regressão em y
não é
paralela ao eixo
dos x.
,
isto é, H.
Alternativa:
a reta de regressão em y
não é
paralela ao eixo
dos x.
SQx = ![]() x2
–
[(
x2
–
[(![]() x)2
/ n]
x)2
/ n]
SQy
= ![]() y2
–
[(
y2
–
[(![]() y)2
/
n]
y)2
/
n]
SP
=![]() (x.y)
– n.
(x.y)
– n. .
.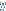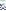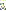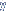
O coeficiente de regressão,
b,
pode ser calculado a partir de várias fórmulas:
b = ![]() [(x
–
[(x
– ![]() )
(y –
)
(y – 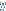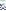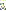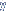 )] /
)] / ![]() (x
–
(x
– ![]() )2
)2
ou
b = (![]() (x.y)
– n.
(x.y)
– n. .
.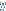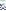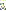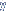 ) /
) / ![]() x2
–
[(
x2
–
[(![]() x)2
/n]
x)2
/n]
ou
b = SP / SQx
O erro de b também pode
ser calculado de maneiras diferentes:
sb = raiz (syx / SQy) ou
sb = raiz {(SQy – b.SP) / [SQx (n – 2)]}
Para se testar a
significância
de b, ou seja, para testar se b pode ser considerado ou não
como significativamente
diferente de zero, calcula-se t, com GL
= n - 2, sendo:
t = b / sb
Para encontrar o t crítico, consulta-se a
tabela
de t, e obedece-se o seguinte
critério:
|
t não é significativo b não é significativamente diferente de 0 (a reta é paralela ao eixo dos x) |
|
t é significativo b é significativamente diferente de 0 (a reta não é paralela ao eixo dos x) |
1. Se t não for significativo os caracteres não estão correlacionados: ( t = 0)
 Se
t
for significativo os caracteres estão correlacionados: (
t
Se
t
for significativo os caracteres estão correlacionados: (
t 0)
0)
2. Sendo
t  0, se b < 0 a correlação é
negativa. Os
caracteres
variam em sentidos opostos.
0, se b < 0 a correlação é
negativa. Os
caracteres
variam em sentidos opostos.
 Sendo
t
Sendo
t  0,
se b > 0 a correlação é
positiva. Os caracteres
variam no mesmo sentido.
0,
se b > 0 a correlação é
positiva. Os caracteres
variam no mesmo sentido.
 |
 |
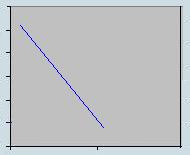 |
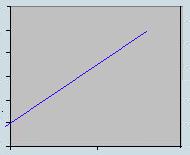
| ausência de correlação | correlação positiva | correlação negativa |
| t = 0, qualquer b | t 0,
b > 0 0,
b > 0 |
t 0,
b < 0 0,
b < 0 |
| Não há sentido de variação | As
variáveis variam no mesmo sentido |
As
variáveis variam em sentidos opostos |
Exemplo: Os seguintes dados foram obtidos amostrando
dimensões do mesmo órgão de 10
indivíduos.
| comprimento | x | 40 | 25 | 65 | 75 | 65 | 40 | 50 | 40 | 15 | 25 |
| largura | y | 25 | 15 | 50 | 65 | 50 | 25 | 40 | 40 | 15 | 15 |
| 440 | 340 |
n
|
10
|
||||
 |
44 | 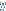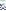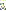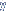 |
34 |
|
17950
|
||
| 22850 |
|
14350 |
n.
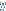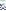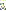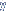 |
14960
|
|||
| 19360 |
|
11560 |
SP
|
2990
|
|||
|
SQx
|
3490 |
SQy
|
2790 |
SP2
|
8940100
|
||
|
s2x
|
387,78 | s2y | 310 |
Exercício:
Confira os cálculos abaixo e complete
as seguintes frases:
1. Existe
correlação
entre os caracteres da amostra? Porque?
b = SP / SQx = 2990 / 3490 = 0,86
sb
=
raiz
(SQy - b.SP) / [SQx (n -2)]
 = raiz
(2790 - 0,86 2990) / [3490 (10 -2)]
= 0,09
= raiz
(2790 - 0,86 2990) / [3490 (10 -2)]
= 0,09
t = b / sb = 0,86 / 0,09 = 9,556.
Após ter o valor de t, consulta-se a tabela de t para se chegar ao valor de tc.
Sendo que: G.L. = _____________ tc = _____________ com P ___ 0,001
Resposta:
Sendo t = ____________
sua probabilidade é _____________ . Como t é
_____________ (maior - menor) que tc ( tc
= _____________ ), conclui-se que t _____________ (é -
não é) significativo, portanto,
_________ (há - não há)
correlação entre as
variáveis
x e y.
Como b é _____________ (igual a - diferente de)
zero, a reta
será _____________ (paralela - não paralela) ao
eixo dos x e
_____________ (ascendente - descendente), já que b
é
_____________
(positivo - negativo).
2. Qual o sentido da
variação
desses caracteres?
A correlação é _____________ (positiva - negativa) , pois b ( _____________ ) é _____________ (positivo - negativo). Portanto, o comprimento e a largura desse órgão variam _____________ (no mesmo sentido - em sentidos postos), ou seja são ______________________ (diretamente - inversamente) proporcionais.
3. Qual a reta de
regressão
que melhor se ajusta aos dados da amostra?
Atribui-se 2 valores extremos de x,
e substitui-se em y = 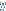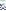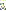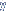 + b.(x -
+ b.(x -  )
. Por exemplo:
)
. Por exemplo:
para
x = 10, y = 34 +
0,86.(10
- 44) = 4,8 e
para x = 80, y = 34 +
0,86.(80
- 44) = 65,0
Com esses valores crie o melhor gráfico que representa esses
dados. (Veja como clicando aqui).
|
Regressão e Correlação Copie a planilha comprimida em formato livre ods |
| r = | n
. |
| r = | (  . .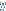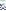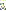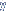 ) / [( n - 1).
) / [( n - 1).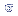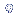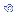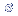 x. x.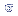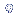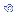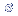 y] y] |
| r = | raiz ( b.SP / SQy ) |
| r = | b.(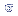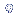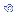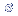 x
/ x
/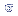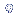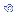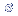 y) y) |
Observando
as duas últimas
fórmulas
rapidamente percebe-se que se não houver
correlação
entre x e y, ou seja, se r = 0, então b
= 0 e a reta
será
paralela ao eixo dos x.
O coeficiente r
varia entre
-1 e +1. Portanto, a correlação pode ser:
| -1 | -0,95 | -0,50 | -0,10 |
|
0,10 | 0,50 | +0,95 | +1 |
| neg | neg | neg | neg | ausência | pos | pos | pos | pos |
| perfeita | forte | moderada | fraca | fraca | moderada | forte | perfeita |
Para testar a significância
usamos um teste t. Estabelecemos as
hipóteses:
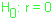 ,
ou seja, H.
Nula:
Não há correlação entre as
variáveis
x e y.
,
ou seja, H.
Nula:
Não há correlação entre as
variáveis
x e y.
 ,
isto é, H.
Alternativa:
Há correlação entre as
variáveis x e
y.
,
isto é, H.
Alternativa:
Há correlação entre as
variáveis x e
y.
Calcula-se
t, com GL
= n-2, por meio da seguinte fórmula:
t = r .
raiz
[(N - 2) / (1 - r2 )]
O coeficiente de
determinação
é simbolizado por r2
e indica quanto
da variação total é comum aos
elementos que
constituem os pares analisados.
Assim, a qualidade da regressão
é
indicada por este coeficiente.
É importante notar que r2
varia entre 0 (zero) e 1 (um).
Evidentemente, quanto mais próximo da unidade
for o coeficiente de Determinação, tanto
maior será a validade da regressão.
Exemplo 1:
Supondo que numa certa
amostra tivessem sido obtidos os seguintes valores:
b = 0,86; SP = 2990; SQy = 2790
Estima-se r = raiz
(
b.SP / SQy ), r =
raiz
(
0,86.2990 /
2790), r =
0,96
Portanto, r2 = 0,92
1 - 0,92 = 0,08, ou seja 8%
Assim,
pode-se dizer que apenas
8%
da variância da regressão não depende
das
variáveis
estudadas.
Exemplo 2:
Dados obtidos de 7
pares de pai-filho, amostrando o número de anos de escola
cursados pelo pai (x) e o número de anos de escola cursados
pelo
filho (y).
Qual é o valor do coeficiente de
correlação entre
esses dados? Qual é o seu significado?
| x | x2 | y | y2 | x.y |
| 12 | 144 | 12 | 144 | 144 |
| 10 | 100 | 8 | 64 | 80 |
| 6 | 36 | 6 | 36 | 36 |
| 16 | 256 | 11 | 121 | 176 |
| 8 | 64 | 10 | 100 | 80 |
| 9 | 81 | 8 | 64 | 72 |
| 12 | 144 | 11 | 121 | 132 |
r = N
.![]() xy
- (
xy
- (![]() x)
(
x)
(![]() y)
/raiz
[ N.
y)
/raiz
[ N.![]() x2
-
(
x2
-
(![]() x)2
]
[ N.
x)2
]
[ N.![]() y2
-
(
y2
-
(![]() y)2
]
y)2
]
r = 7 . 720 - 73 . 66
/ raiz [ 7 . 825 - (73)2 ]
[ 7
. 650 - (66)2 ]
r = + 0,754
Para testar a
significância
usamos um teste t. Estabelecemos as hipóteses:
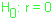 e
e 
t = r . raiz [(N - 2) / (1 - r2 )]
t
= [+ 0,754. raiz[(7-2)] / (1
- 0,7542
)],
portanto,
t
= 2,581
Verificando a tabela
de t, com GL = 5 e
a = 5%, t5 = 2,571
Conclui-se que como
t calculado é
maior
que tc, pode-se rejeitar a hipótese
nula ( r
=
0 ) e aceitar a hipótese alternativa em que r![]() 0,
admitindo-se que o número de anos de escola cursados pelo
pai
está
positivamente correlacionado ( r = + 0,754 ) ao
número
de
anos de escola cursados pelo filho nesta amostra.
0,
admitindo-se que o número de anos de escola cursados pelo
pai
está
positivamente correlacionado ( r = + 0,754 ) ao
número
de
anos de escola cursados pelo filho nesta amostra.
Como r2
=
0,5685 e 1 - 0,5685 = 0,4315, pode-se dizer que nessa
amostra, o
número
de anos de escola cursados pelo pai explica 56,85% da
variância
do
número de anos de escola cursados pelo filho. Assim, 43,15%
da
variância
da regressão depende de outras variáveis,
não
estudadas aqui.
|
|
|
|
|
|
Obtém-se
o coeficiente de
associação
Q por meio de:
Q = (ad - bc) / (ad + bc)
O desvio padrão de Q é obtido por:
s = (1 - Q2 ) / 2 raiz (1/a + 1/b + 1/c +1/d)
O intervalo de confiança de 95% de Q é obtido por:
Q ± t.s
Exemplo:
Supondo que a
distribuição
de 200 pacientes adultos (92 homens e 108 mulheres) segundo as formas
maligna
e benigna de uma doença foi:
| Forma / Sexo |
|
|
|
| Maligna |
|
|
|
| Benigna |
|
|
|
| Total |
|
|
|
em
que:
y = é a estimativa da
variável
dependente
x = variável independente
a = constante = intercepto
múltiplo
b = constante = coeficientes de
regressão
A
análise
de
regressão
múltipla é trabalhosa pois
envolve a
construção
e multiplicação de matrizes tanto maiores quanto
maior
for
o número de variáveis independentes analisadas.
Assim,
é
necessário realizar tal análise em computadores.
Portanto,
aqui nos preocupamos com a interpretação de
resultados de
análise de regressão múltipla.
Exemplo
Em uma amostra de 36
hansenianos de sexo masculino tentou-se verificar se a quantidade de um
certo medicamento presente no sangue 6 hs após a sua
ingestão
(variável dependente) está correlacionada com
idade, peso
corporal, duração da doença, anos de
sulfonoterapia,
valor do hematócrito, taxa de hemoglobina, nível
de
globulinas
e nível de albumina (variáveis independentes).
| Quantidade do medicamento no sangue, após 6 hs de ingestão |
|
|
|
|
|
| x1 | idade |
-0,0586
|
0,0542
|
-1,081
|
> 0,20
|
| x2 | peso corporal |
-0,0145
|
0,0374
|
-0,388
|
> 0,60
|
| x3 | duração da doença |
-0,0115
|
0,0468
|
0,246
|
> 0,80
|
| x4 | anos de sulfonoterapia |
-0,0894
|
0,0520
|
1,719
|
> 0,05
|
| x5 | valor do hematócrito |
-0,2317
|
0,0990
|
-2,340
|
<
0,05
|
| x6 | taxa de hemoglobina |
0,00005
|
0,0318
|
0,002
|
> 0,90
|
| x7 | nível de globulinas |
0,0695
|
0,0876
|
0,793
|
> 0,40
|
| x8 | nível de albumina |
-0,0079
|
0,0601
|
-0,131
|
> 0,80
|
Conclui-se que o
nível
sangüíneo
desse medicamento, após 6 hs de ingestão depende
apenas
da variável x5,
valor do hematócrito, pois entre
todos os coeficientes de regressão calculados somente o b
(-0,2317)
dessa variável é significativamente diferente de
zero
(pois
t(27) = -2,340), que determina uma
probabilidade menor que
0,05.
Um cuidado a ser tomado antes de se realizar uma análise de regressão múltipla é calcular os coeficientes de correlação de todas as variáveis tomadas aos pares. Sabe-se que se houver duas ou mais variáveis com coeficientes de correlação muito altos (r igual ou superior a 0,95) elas interferirão nos cálculos de regressão múltipla. Se forem encontradas 2 ou mais variáveis nessa condição deve-se escolher apenas uma delas para o processamento da análise de regressão múltipla.
t = (b / sb)
A tabela que se segue mostra o resultado
da análise de regressão múltipla
escalonada aplicada
aos mesmos dados que foram usados para a tabela anterior.
| Qtdd
do medicamento
no sangue após 6 hs de ingestão |
|
cimo |
|
|
|
|
|
| x5 | valor do hematócrito |
0,1750
|
---------
|
-0,2317
|
0,0990
|
-2,340
|
<
0,05
|
| x4 | anos de sulfonoterapia |
0,3133
|
0,1383
|
-0,0894
|
0,0520
|
1,719
|
> 0,05
|
| x3 | duração da doença |
0,3155
|
0,0022
|
-0,0115
|
0,0468
|
0,246
|
> 0,80
|
| x7 | nível de globulinas |
0,3472
|
0,0317
|
0,0695
|
0,0876
|
0,793
|
> 0,40
|
| x2 | peso corporal |
0,3613
|
0,0141
|
-0,0145
|
0,0374
|
-0,388
|
> 0,60
|
| x8 | nível de albumina |
0,3615
|
0,0002
|
-0,0079
|
0,0601
|
-0,131
|
> 0,80
|
| x6 | taxa de hemoglobina |
0,3517
|
0,0002
|
0,00005
|
0,0318
|
0,002
|
> 0,90
|
| x1 | idade |
0,3882
|
0,0265
|
-0,0586
|
0,0542
|
-1,081
|
> 0,20
|
|
Copie
esse texto em formato
pdf Depois, clique em"Salvar destino como" (ou algo semelhante ) Escolha o local onde salvar e clique em OK. |
|
Este "site", destinado
prioritariamente
aos alunos de Fátima Conti,
está disponível sob FDL (Free
Documentation Licence),
pretende auxiliar quem se interessa por Bioestatística,
estando em permanente
construção.
Sugestões e
comentários
são bem vindos.
Se desejar colaborar
clique
aqui.
Agradeço
antecipadamente.

Deseja enviar essa página?
Se você usa um programa
de correio eletrônico devidamente configurado para
um e-mail
pop3, clique em "Enviar página" (abaixo) para
abrir o
programa.
Preencha o endereço
do destinatário da mensagem.
E pode acrescentar o que quiser.
(Se não der certo,
clique aqui
para saber mais).

Se você usa webmail
copie o endereço abaixo
http://www.cultura.ufpa.br/dicas/biome/bioreg.htm
Acesse a página do seu provedor. Abra uma nova mensagem.
Cole o endereço no campo de texto.
Preencha o endereço do destinatário.
E também pode acrescentar o que quiser.
Última
alteração: 8 nov 2011