
 Biometria
BiometriaPara visualizar corretamente configurar a tela para 1024 x 768 pixels

 Biometria
Biometria , é
um teste de hipóteses que se destina a
, é
um teste de hipóteses que se destina a encontrar
um
valor da dispersão para duas
variáveis nominais,
e
encontrar
um
valor da dispersão para duas
variáveis nominais,
e  avaliar
a associação
existente entre variáveis qualitativas.
avaliar
a associação
existente entre variáveis qualitativas. Verificar se a
frequência
com que um determinado acontecimento observado em uma amostra se desvia
significativamente ou não da frequência
com que ele
é
esperado.
Verificar se a
frequência
com que um determinado acontecimento observado em uma amostra se desvia
significativamente ou não da frequência
com que ele
é
esperado. Comparar a
distribuição
de diversos acontecimentos em diferentes amostras, a fim de avaliar se
as proporções observadas destes eventos mostram
ou
não
diferenças significativas ou se as
amostras diferem
significativamente
quanto às proporções desses
acontecimentos.
Comparar a
distribuição
de diversos acontecimentos em diferentes amostras, a fim de avaliar se
as proporções observadas destes eventos mostram
ou
não
diferenças significativas ou se as
amostras diferem
significativamente
quanto às proporções desses
acontecimentos. Os
grupos devem
ser independentes,
Os
grupos devem
ser independentes, Os
itens de cada grupo
são selecionados
aleatoriamente,
Os
itens de cada grupo
são selecionados
aleatoriamente, As
observações devem ser
frequências ou contagens,
As
observações devem ser
frequências ou contagens, Cada
observação pertence a
uma e somente uma categoria e
Cada
observação pertence a
uma e somente uma categoria e A
amostra deve ser
relativamente grande (pelo
menos 5
observações em cada célula e, no caso
de poucos
grupos, pelo menos 10. Exemplo: em tabelas 2x 2).
A
amostra deve ser
relativamente grande (pelo
menos 5
observações em cada célula e, no caso
de poucos
grupos, pelo menos 10. Exemplo: em tabelas 2x 2).  =
= [(o - e)2 /e]
[(o - e)2 /e]
 o
= frequência
observada para cada classe,
o
= frequência
observada para cada classe,
 e
=
frequência
esperada para aquela classe.
e
=
frequência
esperada para aquela classe. =
= (d2
/e)
(d2
/e)
 é
pequeno.
Mas, quando as divergências são
grandes (o - e) passa a ser também grande e,
consequentemente,
é
pequeno.
Mas, quando as divergências são
grandes (o - e) passa a ser também grande e,
consequentemente,  assume
valores altos.
assume
valores altos.
 Hipótese nula:
As
frequências observadas não
são diferentes das frequências
esperadas. Não existe diferença
entre as
frequências (contagens) dos grupos.
Hipótese nula:
As
frequências observadas não
são diferentes das frequências
esperadas. Não existe diferença
entre as
frequências (contagens) dos grupos.
Portanto,
não
há associação entre os grupos
 Hipótese
alternativa: As frequências
observadas
são diferentes da
frequências
esperadas, portanto existe diferença entre as
frequências.
Hipótese
alternativa: As frequências
observadas
são diferentes da
frequências
esperadas, portanto existe diferença entre as
frequências.
Portanto, há
associação entre os
grupos.
É
necessário
obter duas estatísticas denominadas  calculado
e
calculado
e 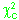 tabelado.
(Para ver a
tabela de
tabelado.
(Para ver a
tabela de ,
clique
aqui).
,
clique
aqui).
As frequências observadas são obtidas
diretamente dos
dados das amostras, enquanto que as frequências
esperadas
são calculadas a partir destas.
Assim, o  calculado
é obtido a partir dos dados
experimentais, levando-se em
consideração os valores observados e os
esperados, tendo em vista a hipótese.
calculado
é obtido a partir dos dados
experimentais, levando-se em
consideração os valores observados e os
esperados, tendo em vista a hipótese.
Já o tabelado
depende do número de graus de liberdade e do
nível de significância adotado.
tabelado
depende do número de graus de liberdade e do
nível de significância adotado.
A tomada de
decisão é feita comparando-se os dois
valores
de  :
:
 Se
Se
 calculado >
ou =
calculado >
ou = 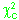 tabelado:
Rejeita-se Ho.
tabelado:
Rejeita-se Ho.
 Se
Se
 calculado
<
calculado
< 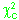 tabelado:
Aceita-se Ho.
tabelado:
Aceita-se Ho.
Quando se consulta a tabela
de  observa-se que é determinada uma probabilidade
de ocorrência daquele acontecimento.
observa-se que é determinada uma probabilidade
de ocorrência daquele acontecimento.
Portanto, rejeita-se
uma hipótese quando a máxima probabilidade de
erro ao rejeitar aquela hipótese for baixa (alfa baixo). Ou,
quando a probabilidade dos desvios terem ocorrido pelo simples acaso
é baixa.
O nível
de
significância (alfa) representa a
máxima
probabilidade de erro que se tem ao rejeitar uma
hipótese.
O número de graus
de liberdade, nesse caso é assim calculado:
G.L. = número de classes - 1
E, evidentemente, quanto
maior for o valor do  mais
significante é a relação entre a
variável dependente e a variável independente.
mais
significante é a relação entre a
variável dependente e a variável independente.
Exemplo 1:
Se uma moeda
não
viciada for jogada 100 vezes, espera-se obter 50 caras e 50 coroas,
já
que a probabilidade de cair cara (p) é
= ½ e a
de cair coroa (q) também é = ½.
Entretanto,
na prática,
é muito difícil obter valores observados,
idênticos
aos esperados, sendo comum encontrar valores que se desviam dos
teóricos.
Supondo que uma moeda foi jogada 100 vezes e se
obteve 60 caras e 40 coroas.
a. Qual será o valor de ![]() ?
?
b. Como se pode interpretar esse valor?
Resolvendo:
As frequências esperadas em cada classe são calculadas por: p.N. Portanto:
E(cara) = ½ .100 e E(coroa) = ½ .100
Assim, os valores esperados são: cara: 50 e coroa: 50 e os observados são: cara: 60 e coroa: 40.
![]() =
[(60 – 50)2 / 50] + [(40 –
50)2 / 50]
=
[(60 – 50)2 / 50] + [(40 –
50)2 / 50]
a. Valor de ![]() =
2 + 2 = 4
=
2 + 2 = 4
| O
que significa esse número? Ou seja, como se
analisa um teste
de Supondo que em
vez de lançarmos
100 moedas uma única vez, tivéssemos feito
inúmeros
lançamentos de 100 moedas. Se calcularmos o Nota-se que os
valores pequenos
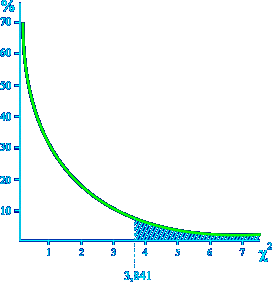
de Tomando a área total sob a curva
como 100%, sabe-se que o valor 3,841 delimita 5% dela. Este
é o valor crítico de
qui quadrado
conhecido como Sempre que o valor de |
 |
b. Como se pode interpretar esse valor?
No exemplo dado, como o valor de Qui Quadrado obtido ( 4 ) para 2 classes foi maior que o esperado ao acaso (3,841), aceita-se a hipótese alternativa e admite-se que a moeda seja viciada.
Entretanto, é importante notar que esse
raciocínio e decisão
só
são válidos quando há
2 classes possíveis de
eventos.
(Como no exemplo dado, em que o lançamento da moeda pode
resultar em
2 acontecimentos: cara ou coroa).
Mas, se tivéssemos lançado um dado seriam 6 classes possíveis. Como faríamos, então?
Deve-se consultar uma tabela de ![]() e
lembrar que, nesse caso:
e
lembrar que, nesse caso:
G.L. = número de classes - 1
A tabela de Qui Quadrado mostra o número de Graus
de liberdade nas linhas e o valor da Probabilidade
nas colunas.
Na coluna referente a 5% de
probabilidade encontra-se o valor
crítico de
qui quadrado (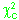 ),
com o qual deve ser comparado o valor calculado de
),
com o qual deve ser comparado o valor calculado de .
.
GL
\
P
|
0,99 |
0,95 |
0,90 |
0,80 |
...
|
|
0,02
|
0,01
|
0,001
|
| 0,05 | |||||||||
| 1 | 0,0002 | 0,004 | 0,016 | 0,064 | ... |
3,841
|
5,412
|
6,635
|
10,827
|
| 2 | 0,020 | 0,103 | 0,211 | 0,446 | ... |
5,991
|
7,824
|
9,210
|
13,815
|
| 3 |
0,115 | 0,352 |
0,584 |
1,005 |
... | 7,815 | 9,837 | 11,345 | 16,266 |
| 4 | 0,297 | 0,711 | 1,064 | 1,649 | ... | 9,488 | 11,668 | 13,277 | 18,467 |
| 5 | 0,554 | 1,145 | 1,610 | 2,343 | ... | 11,070 | 13,388 | 15,080 | 20,515 |
| ... | |||||||||
| Conclusão | Aceita-se
a hipótese de igualdade estatística entre os números de observados e de esperados (H0). Os desvios não são significativos. |
Rejeita-se
H0 e aceita-se H1. Os números de obs e esp são estatisticamente diferentes. Os desvios são significativos. |
|||||||
| Face 1 | Face 2 | Face 3 | Face 4 | Face 5 | Face 6 |
| 34 | 29 | 30 | 32 | 28 | 33 |
E(face 1) = E(face 2) = E(face 3) = E(face 4) = E(face 5) = E(face 6) = p.N = 1 / 6 .186 = 31
a. Qual será o valor de ![]() ?
?
Assim, os valores parciais são somados: e chega-se
ao valor de ![]() :
:
| observado | 34 | 29 | 30 | 32 | 28 | 33 |
| esperado | 31 | 31 | 31 | 31 | 31 | 31 |
| 0,2903 | 0,1290 | 0,0322 | 0,0322 | 0,2903 | 0,1290 |
![]() = (
0,2903 + 0,1290 + 0,0322 + 0,0322
+ 0,2903 + 0,1290) = 0,903
= (
0,2903 + 0,1290 + 0,0322 + 0,0322
+ 0,2903 + 0,1290) = 0,903
 na linha em G.L. = 5
encontra-se
na linha em G.L. = 5
encontra-se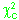 igual a
11,070. Como o valor de Qui
Quadrado obtido
igual a
11,070. Como o valor de Qui
Quadrado obtido|
Qui Quadrado, com
até 4 classes, havendo proporções
esperadas |
 pode
ser aplicado em casos em que não se dispõe de uma
teoria que
permita efetuar o cálculo de classes esperadas.
pode
ser aplicado em casos em que não se dispõe de uma
teoria que
permita efetuar o cálculo de classes esperadas.
 Hipótese nula, H0:
Não há associação entre os
grupos, ou seja, as variáveis são independentes.
Hipótese nula, H0:
Não há associação entre os
grupos, ou seja, as variáveis são independentes.
 Hipótese
alternativa, Ha:
Há associação entre os
grupos, ou seja, as variáveis
são dependentes.
Hipótese
alternativa, Ha:
Há associação entre os
grupos, ou seja, as variáveis
são dependentes.
O número de graus de liberdade, quando os dados estão em tabela de contingência é assim calculado:
G.L. =
número de
linhas - 1 x número de colunas - 1
 calculado
e
calculado
e tabelado.
(Para ver a
tabela de
tabelado.
(Para ver a
tabela de ,
clique
aqui).
,
clique
aqui).
 : Se
: Se  calculado
>
ou =
calculado
>
ou = 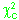 tabelado:
Rejeita-se Ho.
tabelado:
Rejeita-se Ho.
 Critério:
Critério:
 Se
Se  calculado
<
calculado
< 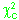 tabelado:
Aceita-se Ho.
tabelado:
Aceita-se Ho.
| AMOSTRA | Reação + | Reação - | Total |
| Crianças | 25 | 45 | 70 |
| Jovens | 15 | 25 | 40 |
| Adultos | 10 | 30 | 40 |
| Total | 50 | 100 | 150 |
Para calcular os
esperados
multiplica-se os totais parciais relativos a cada casela e divide-se
pelo
total geral (N).
Por exemplo, na casela crianças + = 50 x 70 / 150 = 23,3333
Depois calcula-se os qui quadrados parciais.
Por exemplo, na casela
crianças + = (o-e)2
/e = [(25 -
23,3333)2 /
23,3333)] = 0,1190.
Depois, calcula-se a
parcela
de  referente
a cada casela.
referente
a cada casela.
Ao final, soma-se as
parcelas
e obtém-se o  .
.
| Amostra | Reação + | Reação - | Total |
| Crianças | 25 | 45 | 70 |
| Esp | 23,3333 | 46,6667 | |
| (o-e)2 /e | 0,1190 | 0,0595 | |
| Jovens | 15 | 25 | 40 |
| Esp | 13,3333 | 26,6667 | |
| (o-e)2 /e | 0,2083 | 0,1042 | |
| Adultos | 10 | 30 | 40 |
| Esp | 13,3333 | 26,6667 | |
| (o-e)2 /e | 0,8333 | 0,4167 | |
| Total | 50 | 100 | 150 |
 =
0,1190 + 0,0595 + 0,2083 + 0,1042 + 0,8333 + 0,4167. Portanto,
=
0,1190 + 0,0595 + 0,2083 + 0,1042 + 0,8333 + 0,4167. Portanto,  =
1,7410
=
1,7410
O número de GL em tabelas é
assim calculado:
GL = (número de linhas
-1) x (número de colunas -1).
Portanto:
GL = (2 - 1) x (3 - 1) =
2
Depois, consulta-se a tabela de Qui quadrado e
verifica-se
que![]() = 5,991.
= 5,991.
Como o valor de ![]() obtido
é menor que o
obtido
é menor que o ![]() conclui-se que os desvios não são
significativos.
conclui-se que os desvios não são
significativos.
Portanto, os indivíduos pertencentes às 3 amostras ( crianças, adolescentes e adultos ) reagem do mesmo modo ao teste sorológico, não havendo influência das diferentes faixas etárias sobre o resultado do teste. Assim sendo, o resultado sorológico independe dos grupos etários.
|
Qui Quadrado, em tabelas
de contingência, com ordem até 5 x 5 |
 supõe-se
que o tamanho das amostras seja "grande".
supõe-se
que o tamanho das amostras seja "grande". calculado
é aproximado, pois
calculado
é aproximado, pois significativo
mas
nota-se que a amostra é pequena e/ou
que a
frequência
esperada em uma das classes é pequena (tipicamente,
quando for menor
que 5) a fórmula de obtenção
de
significativo
mas
nota-se que a amostra é pequena e/ou
que a
frequência
esperada em uma das classes é pequena (tipicamente,
quando for menor
que 5) a fórmula de obtenção
de poderá
produzir um valor maior que o real.
poderá
produzir um valor maior que o real. pode
ser usado se o
número de observações em cada
casela da tabela for maior ou igual a 5 e a menor
frequência esperada
for maior ou igual a 5.
pode
ser usado se o
número de observações em cada
casela da tabela for maior ou igual a 5 e a menor
frequência esperada
for maior ou igual a 5. =
= [( | o -e | - 0,5)2/ e
]
[( | o -e | - 0,5)2/ e
] obtido
for menor que
obtido
for menor que
Exemplo 1
Supondo uma coleção
de irmandades, com N = 16, filhos de casais com
um
cônjuge
afetado por uma anomalia endógena.
4 dentre os filhos
também apresentam
a doença.
A característica obedece o
padrão de
transmissão
autossômico, dominante e monogênico?
A genealogia seria:

Em 16 filhos espera-se 8
normais e 8 anormais. Mas foram observados 12 normais e 4 anormais.
Obtém-se o valor de Qui quadrado:
 =
[(12 - 8)2 / 8 + (4 - 8)2
/ 8] = 2 + 2 = 4
=
[(12 - 8)2 / 8 + (4 - 8)2
/ 8] = 2 + 2 = 4
Simplesmente analisando o valor de![]() concluiria-se
que
como é maior que
concluiria-se
que
como é maior que ![]() (3,841) os desvios não são devidos ao acaso.
Portanto,
conclui-se que a doença não obedece o
padrão de
transmissão
autossômico, dominante e monogênico.
(3,841) os desvios não são devidos ao acaso.
Portanto,
conclui-se que a doença não obedece o
padrão de
transmissão
autossômico, dominante e monogênico.
Entretanto, deve-se reparar que:
 N
é menor que 40 e
N
é menor que 40 e
 o
valor de Qui Quadrado
obtido é
maior que o crítico
o
valor de Qui Quadrado
obtido é
maior que o crítico
Portanto, deve-se aplicar a correção de Yates:
![]() =
[ (| o1 - e1
| - 0,5)2
/ e1 +
(| o2 - e2
| - 0,5)2
/ e2)]
=
[ (| o1 - e1
| - 0,5)2
/ e1 +
(| o2 - e2
| - 0,5)2
/ e2)]
![]() =
[( | 12 - 8 | - 0,5)2 / 8 + ( | 4
-8 | - 0,5)2
/ 8)] = 1,51313 + 1,51313 = 3,062
=
[( | 12 - 8 | - 0,5)2 / 8 + ( | 4
-8 | - 0,5)2
/ 8)] = 1,51313 + 1,51313 = 3,062
 <
<
| Sexo / Tem alergia? | Sim | Não | Total |
| Mulheres | 10 | 9 | 19 |
| Homens | 13 | 2 | 15 |
| Total | 23 | 11 | 34 |
Para calcular os
esperados
multiplica-se os totais parciais relativos a cada casela e divide-se
pelo
total geral (N).
Depois calcula-se os qui quadrados parciais
utilizando (o-e)2
/e.
Depois, calcula-se a
parcela
de  referente
a cada casela.
referente
a cada casela.
Ao final, soma-se as
parcelas
e obtém-se o  :
:
| Sexo / Tem alergia? | Tem alergia | Não tem alergia | Total |
| Mulheres | 10 | 9 | 19 |
| Esp | 12,85 | 6,15 | |
| (o-e)2 /e | 0,6333 | 1,3241 | |
| Homens | 13 | 2 | 15 |
| Esp | 10,15 | 4, 85 | |
| (o-e)2 /e | 0,8021 | 1,6772 | |
| Total | 23 | 11 | 34 |
 =
0,6333 + 0,8021 + 1,3241 + 1,6772. Portanto,
=
0,6333 + 0,8021 + 1,3241 + 1,6772. Portanto,  =
4,4367
=
4,4367
Como o número de GL em tabelas 2x2
é GL = (2 - 1) x (2 - 1) = 1, percebe-se que ![]() é 3,841.
é 3,841.
Como ![]() obtido
é maior
que o crítico os desvios não
são devidos ao acaso.
Portanto,
concluiria-se que a alergia depende do sexo.
obtido
é maior
que o crítico os desvios não
são devidos ao acaso.
Portanto,
concluiria-se que a alergia depende do sexo.
Entretanto, deve-se reparar que:
 N
é menor que 40,
N
é menor que 40,
 o
valor de Qui Quadrado
obtido é
maior que o crítico e
o
valor de Qui Quadrado
obtido é
maior que o crítico e
 há
pelo menos
uma classe com número de
esperados menor que 5.
há
pelo menos
uma classe com número de
esperados menor que 5.
Portanto, deve-se aplicar a correção
de Yates: ![]() =
= [( | on - en
| - 0,5)2
/ en )]
[( | on - en
| - 0,5)2
/ en )]
| Amostra | Fuma | Não fuma | Total |
| Mulheres | 10 | 9 | 19 |
| Esp | 12,8529 | 6,1471 | |
| (o-e)2 /e | 0,4307 | 0,9006 | |
| Homens | 13 | 2 | 15 |
| Esp | 10,1471 | 4, 8529 | |
| (o-e)2 /e | 0,5456 | 1,1408 | |
| Total | 23 | 11 | 34 |
 =
0,4307 + 0,5456 + 0,9006 + 1,1408. Portanto,
=
0,4307 + 0,5456 + 0,9006 + 1,1408. Portanto,  =
3,0178
=
3,0178 <
<|
Qui Quadrado, em tabelas
de contingência, |
 o
valor de N
< 20 ou
o
valor de N
< 20 ou 20
< N
< 40 e a menor
frequência esperada for menor que 5.
20
< N
< 40 e a menor
frequência esperada for menor que 5.
|
P
|
|||||||||
| GL / P | 0,99 | 0,95 | 0,90 | 0,80 | ... | 0,05 |
0,02
|
0,01
|
0,001
|
| 1 | . | . | . | . | . | . | . | . | . |
| 2 | . | . | . | . | . | . | . | . | . |
| ... | . | . | . | . | . | ||||
| . | Os
desvios não são
significativos. As variáveis estudadas são independentes. A associação entre as variáveis é devida ao acaso. |
Os
desvios são significativos. As variáveis não são independentes. A associação entre as variáveis estudadas não é devida ao acaso. |
|||||||
Exemplo
Supondo a
presença
de uma determinada enzima em pessoas submetidas a uma
reação
sorológica:
|
Reação |
Enzima |
Total |
|
|
|
Presente |
Ausente |
|
|
+ |
5 a |
1 c |
6 G |
|
- |
0 b |
3 d |
3 H |
|
Total |
5 E |
4 F |
9 I |
P = [( G! H! E! F! ) / I! ] x [1 / ( a! c! b! d! )]
P = [(6! 3! 5! 4!) / 9! ] x [1 / (5! 1! 0! 3!)] = 0,0476 = 4,76%
Como
esse valor é menor
que
5% a hipótese das características serem
independentes
é
rejeitada, dizendo-se que a sua associação
não
é
casual.
Deve-se:
a.
calcular
a probabilidade identicamente ao escrito acima
b.
construir
outra tabela 2x2, subtraindo-se uma unidade dos valores da
diagonal que
contiver o menor número de casos
e adicionando essa unidade aos
valores das caselas da outra diagonal
c. calcular
novamente a probabilidade
d. esse
processo continuará até que se atinja o valor 0
e.
somar todas as probabilidades calculadas
Exemplo
Supondo que os valores obtidos sejam:
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Total | ||||
| 5 | 3 | 8 | P = (8! 7! 7! 8! / 15!) (1 / 5! 3! 2! 5!) | |
| 2 | 5 | 7 | P = 0,1828 | |
| Total | 7 | 8 | 15 | |
| . | ||||
| 6 | 2 | 8 | P = (8! 7! 7! 8! / 15!) (1 / 6! 2! 1! 6!) | |
| 1 | 6 | 7 | P = 0,0305 | |
| Total | 7 | 8 | 15 | |
| . | ||||
| 7 | 1 | 8 | P = (8! 7! 7! 8! / 15!) (1 / 0! 7! 1! 7!) | |
| 0 | 7 | 7 | P = 0,0012 | |
| Total | 7 | 8 | 15 |
P
= 0,1828 + 0,0305 +
0,0012 = 0,2145 = 21,45 %
Nesse caso, como o valor encontrado de P é maior que 5%, a hipótese das características serem independentes é aceita, dizendo-se que a sua associação é casual.
Observação: Em tabelas com mais de 2
colunas ou 2 linhas, ou seja, quando G.L. > 1,
pode-se utilizar o teste de  se o
número de caselas com frequência esperada
inferior a 5 é menor que 20%
do total de caselas e nenhuma frequência esperada
for zero.
se o
número de caselas com frequência esperada
inferior a 5 é menor que 20%
do total de caselas e nenhuma frequência esperada
for zero.
|
Teste Exato de Fisher em tabelas 2 x 2 Copie a planilha comprimida em formato xls ou em ods |
Pode-se testar se amostras diferentes
em uma série de experimentos semelhantes são
homogêneas
ou não.
Nesse caso, calcula-se o ![]() de
cada amostra e o
de
cada amostra e o ![]() do
total delas (
do
total delas (![]() ).
).
Depois, soma-se os ![]() obtidos
para cada amostra (
obtidos
para cada amostra (![]()
![]() ) e da soma se subtrai o valor
obtido para o total de qui quadrados
(
) e da soma se subtrai o valor
obtido para o total de qui quadrados
( ![]() ).
).
O valor final obtido
é
o ![]() de
heterogeneidade.
de
heterogeneidade.
Exemplo
Em 3
amostras
de filhos
de
casais MN, obteve-se:
| Amostras | MM | MN | NN | Total |
| Proporções esperadas | 1/4 |
1/2 |
1/4 |
|
| Belém - PA | 19 | 38 | 23 | 80 |
| Maceió - AL | 18 | 25 | 17 | 60 |
| São Carlos - SP | 8 | 23 | 9 | 40 |
| Total | 45 | 86 | 49 | 180 |
| Amostras | Cálculo do |
GL | ||
| Belém - PA | (19-20)2 /20 + (38-40)2 /40 + (23-20)2 /20 | 0,600 |   3,250 |
2 |
| Maceió - AL | (18-15)2 /15 + (25-30)2 /30 + (17-15)2 /15 | 1,700 | 2 |
|
| São Carlos - SP | ( 8-10)2 /10 + (23-20)2 /20 + ( 9-10)2 /10 | 0,950 | 2 |
|
| Total | (45-45)2 /45 + (86-90)2 /90 + (49-45)2 /45 | 0,534 | = |
2 |
Para
obter a 
 basta
somar os valores de
basta
somar os valores de ![]() obtidos
em cada classe e os seus G.L.:
obtidos
em cada classe e os seus G.L.:
1. Calcula-se o ![]() e GL de cada amostra, inclusive de "Total"
e GL de cada amostra, inclusive de "Total"
2. Soma-se os ![]() obtidos ( esse valor é chamado
obtidos ( esse valor é chamado 
 ) e também os GL
) e também os GL
0,600 + 1,700 + 0,950 = ![]()
![]() = 3,250 e GL
= 2 + 2 + 2 =
6.
= 3,250 e GL
= 2 + 2 + 2 =
6.
3. Subtrai-se o ![]() do "Total" da somatória de
do "Total" da somatória de ![]() ( =
( = 
 -
- ![]()
3,250 - 0,534 = 2,716 e GL = 6 - 2 = 4.
Portanto, ![]() = 2,716.
= 2,716.
Na tabela
verifica-se que ![]() crítico = 9,488.
crítico = 9,488.
Conclui-se que, como o valor de ![]() calculado
é menor que o de
calculado
é menor que o de ![]() aceita-se que os desvios são devidos ao acaso,
não sendo
significativos. Portanto as amostras são
homogêneas.
aceita-se que os desvios são devidos ao acaso,
não sendo
significativos. Portanto as amostras são
homogêneas.
Quando se quer provar se
os dados de uma mostra seguem a distribuição de
Poisson
deve-se:
 reunir em uma
única
classe as que tiverem valores esperados menores que 5
reunir em uma
única
classe as que tiverem valores esperados menores que 5
 calcular os esperados
segundo a distribuição de Poisson
calcular os esperados
segundo a distribuição de Poisson
| Número de vezes em que o evento ocorre: | 0 | 1 | 2 | 3 | 4 | |
| Números esperados de amostras | n/eu | nu/eu | nu2/2.eu | nu31/2.3.eu | nu41/2.3.4.eu |
 calcular a parcela
de
calcular a parcela
de  ,
ou seja [(o-e)2
/e] referente a cada
classe
,
ou seja [(o-e)2
/e] referente a cada
classe
 GL
= número de
classes - 2 ( o total e a média da amostra)
GL
= número de
classes - 2 ( o total e a média da amostra)
Exemplo
Foram
observados
os seguintes números de tripanossomos em 128 campos de um
hemocitômetro
| Tripanossomos | Freq. Obs. | Freq. Esp. |
| 0 | 26 | 21,9 |
| 1 | 37 | 38,7 |
| 2 | 31 | 34,1 |
| 3 | 18 | 20,1 |
| 4 | 10 | 8,9 |
| 5 | 3 | | 3,1 | |
| 6 | 3 | 6 | 0,9 | 4,3 |
| 7 | 0 | | 0,2 | |
| >7 | 0 | | 0,1 | |
| Total | 128 |
| Tripanossomos |
Freq.
Obs.
|
Freq.
Esp.
|
(o-e)2 /e
|
| 0 |
26
|
21,9
|
0,768
|
| 1 |
37
|
38,7
|
0,075
|
| 2 |
31
|
34,1
|
0,282
|
| 3 |
18
|
20,1
|
0,219
|
| 4 |
10
|
8,9
|
0,136
|
| > 5 |
6
|
4,3
|
0,672
|
| Total |
128
|
128,0
|
 =
2,152 =
2,152 |
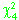 crítico = 9,488.
crítico = 9,488.
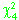 encontrado é menor que o
encontrado é menor que o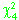 crítico conclui-se que os desvios não
são
significativos.
Portanto, pode-se aceitar que o número de tripanossomos
encontrado
segue a distribuição de Poisson.
crítico conclui-se que os desvios não
são
significativos.
Portanto, pode-se aceitar que o número de tripanossomos
encontrado
segue a distribuição de Poisson.Até algumas décadas atrás, quando não se usava calculadoras ou computadores, eram utilizadas maneiras de efetuar cálculos em alguns tipos de tabelas que facilitavam em muito a obtenção de resultados, por efetuarem menor número de operações.
Assim,
quase que só por
curiosidade, alguns estão especificados aqui.
|
Copie
esse texto em formato
pdf Depois, clique em"Salvar destino como" (ou algo semelhante ) Escolha o local onde salvar e clique em OK. |
|
Este "site", destinado prioritariamente
aos alunos de Fátima Conti,
está disponível sob FDL (Free
Documentation Licence),
pretende auxiliar quem se interessa por Bioestatística,
estando em permanente
construção.
Sugestões e
comentários
são bem vindos.
Se desejar colaborar
clique
aqui.
Agradeço
antecipadamente.

Deseja enviar essa página?
Se você usa um
programa
de correio eletrônico devidamente configurado para
um e-mail
pop3, clique em "Enviar página" (abaixo) para
abrir o programa.
Preencha o endereço
do destinatário da mensagem.
E pode acrescentar o que quiser.
(Se não der certo,
clique aqui
para saber mais).

http://www.cultura.ufpa.br/dicas/biome/bioqui.htm
Acesse a página do seu provedor. Abra uma nova mensagem.
Cole o endereço no campo de texto.
Preencha o endereço do destinatário.
E também pode acrescentar o que quiser.
Última alteração: 29 out 2011