Biometria
Para visualizar corretamente configurar a tela para 1024 x 768 pixels

Probabilidade

(Leitura complementar ao capítulo 2)

Sumário:

Definição
Distribuição de Poisson
Eventos repetidos
Espaço amostral
Ocorrência de 1 evento
Ocorrência de 2 eventos - E
Ocorrência de 2 eventos - OU
Probabilidade condicional


Definição


No século XVII os matemáticos franceses Pierre de Fermat (1601-1665) e Blaise Pascal (1623-1662) iniciaram estudos sobre a teoria dos jogos.

O objetivo principal era prever um resultado e obter êxito em suas apostas.

Mas, seja nos jogos ou em qualquer outro experimento aleatório é possível associar uma medida para a incerteza quanto à ocorrência, ou não, de algum evento.

Essa medida é chamada de probabilidade.

A probabilidade de um acontecimento ocorrer é definida como o quociente do número de eventos desejados pelo total de eventos possíveis (que constitui o espaço amostral).

Probabilidade = número de eventos desejados / número de eventos possíveis

Ocorrência de 1 evento

Assim, a probabilidade de ocorrência de um evento é representada como um número real no intervalo que contém os limites 0 e 1, pois:

para eventos em que a ocorrência é garantida, dizemos que sua probabilidade é igual a 1 (um), ou seja, há certeza de ocorrência do acontecimento e,

para eventos que nunca ocorrerão a sua probabilidade é avaliada como 0 (zero), pois há impossibilidade da ocorrência


não ocorrência possibilidade de ocorrência certeza de ocorrência
P = 0 qualquer valor entre 0 e 1 P = 1

Evidentemente, quanto mais próxima de 1 for a probabilidade de um evento, é mais provável que o evento ocorra.

E ocorre o inverso quando se toma resultados com valor de probabilidade próximos a zero: eles tem ocorrência mais improvável.

Entretanto, deve-se ressaltar que, quando se trata de um evento possível ele pode ocorrer com diferentes probabilidades ( por exemplo: 12%, 53% 94%, etc) podendo aceitar valores desde muito próximos à impossibilidade de ocorrência (por exemplo: 0.01%) até quase atingir a certeza de acontecimento (por exemplo: 99%).

Já, se dois eventos forem ditos como igualmente prováveis, pode-se exprimir a probabilidade de cada evento como "1 em 2", ou, "50%", ou ainda "1/2".


Exemplo 1

No lançamento de uma moeda não viciada, qual a probabilidade de cair coroa?

número de eventos desejados = 1 (só há uma face coroa)
número de eventos possíveis = 2 (há 2 faces na moeda).
Portanto, P = 1/2
Nesse caso os eventos são chamados de equiprováveis.

Caso idêntico a esse é o sexo de criança esperada após uma gravidez: P(menina) = 1/2 e P(menino) = 1/2.


Exemplo 2

No lançamento de um dado não viciado, qual a probabilidade de cair face 4?

número de eventos desejados = 1 (só há uma face 4)
número de eventos possíveis = 6 (há 6 faces no dado).
Portanto, P = 1/6

Exemplo 3

Supondo um casal, em que ambos são homozigotos dominantes para uma certa característica, qual a probabilidade de terem uma criança também homozigota AA?

A resposta é P (AA) = 1 ou 100%. Ou seja, existe 100% de chance da criança ser AA.

Entretanto, e se a pergunta para o mesmo casal, fosse:

Qual a probabilidade da criança ser homozigota aa?

A ocorrência do evento (aa) tem probabilidade igual a zero, P (aa) = 0, pois não há genes a na família.


Ocorrência de 2 eventos

1. Probabilidade de ocorrência de um OU outro acontecimento


Dois eventos são mutuamente exclusivos quando a ocorrência de um impede a ocorrência do outro e vice-versa.

A probabilidade de ocorrerem eventos mutuamente exclusivos é dada pela soma das probabilidades isoladas de ocorrência de cada um dos eventos.

Exemplos

a. Qual a probabilidade de cair face 3 ou face 6 em um único lançamento de dado?

P(3) = 1/6 P(6) = 1/6
P(3 ou 6) = 1/6 + 1/6 = 2/6 = 1/3

b. Qual a probabilidade de se retirar uma dama de um baralho previamente embaralhado?

P (dama copas) = P (dama ouro) = P (dama espadas) = P (dama paus) = 1/52

Portanto, P (dama) = 1/52 + 1/52 + 1/52 + 1/52 = 4/52 = 1/13


2. Probabilidade de ocorrência de um E outro acontecimento

Dois eventos são independentes quando a ocorrência de um não influencia a probabilidade do outro ocorrer.

A probabilidade de ocorrerem eventos independentes é dada pela multiplicação das probabilidades isoladas de ocorrência de cada um dos eventos.


Condição 1: Os acontecimentos são iguais.

Exemplo

Qual a probabilidade de caírem 2 faces 3 no lançamento de 2 dados?

P (3) = 1/6
Logo, P (3 e 3) = 1/6 X 1/6 = 1/36


Condição 2: Os acontecimentos são diferentes.

Neste caso há que se considerar 2 tipos de situação:

2.1. A ordem de ocorrência dos acontecimentos é importante.

Exemplo

Qual a probabilidade de, em 2 lançamentos, cair face 1 no primeiro e face 2 no segundo?

Quais são os eventos possíveis?


Espaço amostral

O espaço amostral, simbolizado por S, é o conjunto que contém todos os resultados possíveis de um experimento aleatório.

{1,1 1,2 1,3 1,4 1,5 1,6
2,1 2,2 2,3 2,4 2,5 2,6
3,1 3,2 3,3 3,4 3,5 3,6
4,1 4,2 4,3 4,4 4,5 4,6
5,1 5,2 5,3 5,4 5,5 5,6
6,1 6,2 6,3 6,4 6,5 6,6}

Portanto: P (1) = 1/6 e P(2) = 1/6

P (1 no primeiro dado e 2 no segundo) = P(1,2) = 1/6 x 1/6 = 1/36


2.2. A ordem de ocorrência dos acontecimentos não é importante

Notar que no espaço amostral do exercício anterior (S), há a parcela ( 2,1 ), ou seja, caiu o número 2 no lançamento do primeiro dado e o 1 no outro. Isto não satisfazia a questão.

Mas, se a pergunta fosse: Qual a probabilidade de, em 2 lances, caírem faces 1 e 2?

P ( 1,2 ) = 1/36 P ( 2,1 ) = 1/36

Logo: P ( 1,2 ou 2,1) = 1/36 + 1/36 = 2/36 = 1/18


3. Probabilidade condicional

Considerando o lançamento de um dado, qual a probabilidade de em 1 jogada resultar em um número ímpar e menor que 3?

Menor que três: 1 e 2 e Ímpar = 1. Portanto, apenas o número 1 satisfaz ambas as condições. Assim, P = 1/6

Portanto, a probabilidade do resultado ser um número ímpar e menor que 3 é a interseção desses eventos:

Menor que três: (1, 2) = 2/6 e Ímpar = (1, 3, 5) = 3/6. Assim, P = 1/6 Exemplos:

a. De um baralho de 52 cartas (13 de ouro, 13 de espadas, 13 de copas e 13 de paus) qual é a probabilidade de, ao ser retirada uma carta, ser uma dama de copas?

P = 1/52

b. De um baralho de 52 cartas (13 de ouro, 13 de espadas, 13 de copas e 13 de paus) qual é a probabilidade de, ao ser retirada uma carta, ser uma dama, sabendo-se que a carta retirada é de copas.

Como há 4 tipos : P = 1/52 X 1/4

Como já se sabe que a carta é de copas, temos apenas 1 dama em um total de 13 cartas. A probabilidade é então: P(Q, copas) = 1/13.


4. Ocorrência de eventos repetidos

Se trabalharmos com muitos eventos haverá um grande número de combinações possíveis (evidentemente, se não considerarmos a ordem de sua ocorrência).

Exemplo: No lançamento de 4 moedas, qual a probabilidade de caírem 3 caras e 1 coroa?


Espaço amostral ( S )

Como foi visto acima:

ca ca ca ca ca ca ca co ca ca co ca ca co ca ca
ca co co co ca ca co co ca co ca co ca co co ca
co ca ca ca co co co ca co co ca ca co ca ca co
co ca co ca co ca co co co co ca co co co co co

Ou seja, há 16 combinações possíveis e, entre elas há 4 que satisfazem a pergunta.

Quando se monta o espaço amostral fica claro que a probabilidade de ocorrência do 3 caras e 1 coroa no lançamento de 4 moedas é

P = 4/16 = 1/4  ou  25%

Entretanto, a construção do espaço amostral pode ser muito trabalhosa.

Como calcularíamos essa probabilidade, com o uso de fórmulas?

Há 2 modos:


1. Casos Complexos: combinações

Quantas combinações com 3 caras e 1 coroa são possíveis?

Este número pode ser calculado pela seguinte fórmula: C = n! / ( x!.y! ). Como y = (n-x). Portanto:

C = n! / [ x! . (n - x)! ]

em que:
n = número total de ocorrência dos eventos
! = fatorial
x = número de ocorrência de um dos eventos (nesse exemplo = cara )

Lembrar que, como só há 2 eventos, x e y: y = (n-x) .

Portanto, nesse exemplo: C = 4! / [3! x (4-3)!] = 4x3x2x1 / 3x2x1 x 1 = 24 / 6 = 4

Assim, há 4 combinações possíveis, que, como visto anteriormente, são:

ca ca ca co - ca ca co ca - ca co ca ca - co ca ca ca

Levando-se em conta apenas o número de caras e de coroas os 16 tipos de resultados podem ser agrupados em cinco classes, ou seja, com 0, 1, 2, 3 ou 4 resultados coroa, respectivamente com 4, 3, 2, 1 ou 0 resultados cara.

Fórmula para casos complexos

Para o cálculo de uma certa probabilidade, pode-se usar a seguinte fórmula

P = C . px . (1-p) (n-x) em que:

C = número de combinações
p = Probabilidade de ocorrência do evento 1 (nesse exemplo = cara )
q = Probabilidade de ocorrência do evento 2 (nesse exemplo = coroa )
x = Número de vezes em que o evento 1 ocorre
n - x = Número de vezes em que o evento 2 ocorre

Voltando à questão: No lançamento de 4 moedas, qual a probabilidade de caírem 3 caras e 1 coroa?
P(cara) = P(coroa) = 1/2 e Número de combinações = C = 4

P = 4 x (1/2)3 x (1/2)1 = 4 x 1/ 8 x 1/2= 4/16 = 1/4.

Obteve-se, portanto, o mesmo valor visto no espaço amostral.


2. Binômio de Newton e Triângulo de Pascal

Esses resultados também podem ser obtidos pelo desenvolvimento do Binômio de Newton.

Para responder a mesma pergunta anterior (No lançamento de 4 moedas, qual a probabilidade de caírem 3 caras e 1 coroa?) o binômio será:
(p + q )4

A expansão desse binômio gera uma equação em que pode-se usar o Triângulo de Pascal para calcular os coeficientes..

Eles serão 1 : 4 : 6 : 4 : 1.

(p + q)4 = 1 p4q0+ 4 p3q1 + 6 p2q2 + 4 p1q3 + 1 p0q4
1 p4 q0 4 coroas e 0 caras
4 p3q1 3 coroas e 1 cara
6 p2q2 2 coroas e 2 caras
4 p1q3 1 coroa e 3 caras
1 p0q4 0 coroas e 4 caras

Lembrando que p = ocorrência do evento "cara" e de q (ou 1-p), entre os resultados possíveis, a fração que interessa é
4p3 q1 = 4 x 1/ 8 x 1/2= 4/16 = 1/4.

Ou seja, novamente foi obtido o mesmo valor visto no espaço amostral. e quando se utilizou a fórmula para casos complexos.

É importante notar que em Genética, o triângulo é bastante útil em casos de herança quantitativa, determinada por vários pares de genes cumulativos. (Se desejar mais detalhes clicar aqui).


Exemplo 2:

Qual a probabilidade de um casal ter 5 filhos, sendo 3 homens e 2 mulheres?

Resolução 1: Usando a fórmula para casos complexos:

C = 5! / (3! x 2!) = 5x4x3x2x1 / 3x2x1 x 2x1 = 10

Portanto, há 10 modos de nascerem 3 homens e 2 mulheres em 5 gestações:

h h h m m - h h m m h - h h m h m - h m m h h - h m h m h
h m h h m - m m h h h - m h m h h - m h h h m - m h h m h
Assim, P(h) = P(m) = 1/2 e C = 10

Aplicando a fórmula P = C . px . (1-p) (n-x)

P(3h e 2m) = 10 x (1/2)3 x (1/2)2 = 10 x 1/ 8 x 1/4 = 10/32 = 5/16


Resolução 2: Utilizando o Binômio de Newton

Nesse caso a equação é (p + q )5

A expansão do binômio gera uma equação em que pode-se usar o Triângulo de Pascal para calcular os coeficientes da equação.

Os coeficientes encontrados são: 1 : 5 : 10 : 10 : 5 : 1

Portanto, a expansão do binômio gerará:

(p + q)5 = 1 p5q0 + 5 p4q1 + 10 p3q2 + 10 p2q3 + 5 p1q4 + 1 p0q5

1 p5q0 5 homens e 0 mulheres
5 p4q1 4 homens e 1 mulher
10 p3q2 3 homens e 2 mulheres
10 p2q3 2 homens e 3 mulheres
5 p1q4 1 homem e 4 mulheres
1 p0q5 0 homens e 5 mulheres

Assim, a fração que interessa é 10p3 q2

Portanto, P(3h e 2m) = 10 x (1/2)3 x (1/2)2 = 10 x 1/ 8 x 1/4 = 10/32 = 5/16


Média, Variância e Desvio padrão, se a distribuição for binomial

Sendo conhecidos os parâmetros da distribuição binomial (n e p):

Média da população = p = n.p usando o dado de um dos acontecimentos ou
q = n.q utilizando o dado do outro acontecimento
Variância da população = 2 2 = n.p.(1 - p) = n.p.q
Desvio padrão da população = 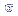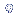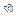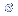= raiz n.p.q


Exemplo

Qual é o número esperado de resultados cara e de resultados coroa em 1000 lances de moeda e seu desvio padrão?

p (cara) = q (coroa) = 0,5
p = n.p = 1000 x 0,5 = 500 caras são esperadas
q = n.q = 1000 x 0,5 = 500 coroas são esperadas
= raiz (n.p.q) = raiz 1000 x 0,5 x 0,5 = 15,81

As últimas fórmulas caracterizam a distribuição binomial de probabilidades para a entidade estatística que está sendo estudada.

É importante notar que para gerar uma distribuição binomial é necessário definir apenas 2 quantidades: n e p, que caracterizam a distribuição de forma exata e são chamadas de parâmetros da distribuição.

Distribuição de Poisson

A distribuição de Poisson pode ser considerada como um caso particular da distribuição binomial, na qual a probabilidade de ocorrência de um dado evento é muito pequena.

Diferentemente da distribuição binomial, que é definida por 2 parâmetros (média e desvio-padrão), a distribuição de Poisson é definida por apenas um, a média, pois a variância é igual à média.

Tomando-se µ = , de acordo com a distribuição de Poisson, as probabilidades de amostras ou subamostras apresentarem 0, 1, 2, 3, 4 ou mais vezes o acontecimento cuja probabilidade de ocorrência é muito pequena, são dadas por:


Número de ocorrências do evento: 0 1 2 3 4
Probabilidade de ocorrência: µ0 / 1eµ µ1 / 1.eµ µ2 / 2.eµ µ3 / 2.3.eµ µ4 / 2.3.4.eµ

1 / eµ µ / eµ
 µ2 / 2.eµ µ3 / 2.3.eµ µ4 / 2.3.4.eµ
Nessas expressões:

. µ = : é a esperança matemática, ou seja, a média esperada de ocorrência de algum acontecimento pouco provável em um conjunto de sub-amostras

. o número irracional e tem valor igual a 2,71828182845904, sendo que seu logaritmo natural é, aproximadamente, 0,434295...

Designando por n o número de subamostras analisadas, e simbolizando por µ, os números esperados de amostras em que o acontecimento pouco provável ocorre 0, 1, 2, 3, 4 ou mais vezes são:
Número de ocorrências do evento: 0 1 2 3 4
Números esperados de amostras n.µ0 / eµ n.µ1 / eµ n.µ2 / 2.eµ n.µ3 / 2.3.eµ n.µ4 / 2.3.4.eµ

n/eµ n.µ/eµ n.µ2/2.eµ n.µ3/2.3.eµ n.µ4/2.3.4.eµ

Quando se quer calcular uma sucessão de valores esperados na distribuição de Poisson, por exemplo: número de amostras com 0, 1, 2, etc, eventos, procede-se do seguinte modo:

1. Aceitar a média, ( ), como o valor paramétrico da distribuição de Poisson,

2. Verifica-se qual é o número de amostras, o qual passa a ser aceito como n,

3. Aplica-se a fórmula para obtenção de amostras com zero eventos: n/eµ
(Note que, usando logaritmos: n/eµ = log n - (µ. log e), onde log e = 0,434295)

4. O antilog do número obtido será o número esperado de amostras com 0 eventos.
Continuando, aplica-se a fórmula para obtenção de amostras com um evento: n.µ / eµ, em que log e = 0,434295

Note que, usando logaritmos, n.µ/eµ = log µ + log n - (µ. log e)

Repare que a parte sublinhada corresponde à primeira fórmula, portanto pode-se tomar o valor ali obtido e lhe acrescentar log µ. Depois, toma-se o antilog do valor encontrado e tem-se o número esperado de amostras com 1 evento.

Continuando, aplica-se a fórmula para obtenção de amostras com dois eventos: n.µ2 / 2.eµ

Note que, usando logaritmos, n.µ2/2.eµ = 2 log µ + log n - (µ. log e + log 2),

Repare que a parte sublinhada corresponde à segunda fórmula, portanto pode-se tomar o valor ali obtido e lhe acrescentar log µ (já que são 2) e diminuir o logaritmo do número de vezes que se deseja o evento (nesse caso log 2) . Depois, toma-se o antilog do valor encontrado e tem-se o número esperado de amostras com 2 eventos.

Continuando, aplica-se a fórmula para obtenção de amostras com três eventos: n.µ3 / 2.3.eµ

Note que, usando logaritmos, n.µ3 / 2.3.eµ = 3 log µ + log n - (µ. log e + log 2 + log 3)

Repare que a parte sublinhada corresponde à terceira fórmula, portanto pode-se tomar o valor ali obtido e lhe acrescentar log µ
(já que são 3) e diminuir o logaritmo do número de vezes que se deseja o evento (nesse caso log 3).

Depois, toma-se o antilog do valor encontrado e tem-se o número esperado de amostras com 3 eventos.

E continua-se com esse raciocínio até atingir o número de vezes desejado.



Logaritmo e antilogaritmo


Dados dois números reais positivos x > 0 e a > 1, chama-se de logaritmo de x na base a o expoente ao qual se deve elevar a base a para se obter o número x.

Assim, a é chamado de base do logaritmo e x é o logaritmando ou antilogaritmo.

Ou seja, um antilogaritmo é a base elevada à potência do número dado.

Exemplo:

Log 78 = 1,8921,

Lembrar que a base 10 não precisa ser escrita. Seria: Log10 78 = 1,8921

Portanto, antilog 1,8921 = 78, pois 101,8921 = 78

O antilogaritmo consiste no inverso do cálculo do logaritmo de um número.


Propriedades básicas dos logaritmos naturais

1. Ln (1) = 0

2. Ln (x.y) = Ln (x) + Ln (y)

3. Ln ( xk ) = k.Ln (x)

4. Ln (x/y) = Ln (x) - Ln (y)


Copie esse texto em formato pdf
clicando no link ao lado com o botão direito do mouse.


Depois, clique em"Salvar destino como" (ou algo semelhante )
Escolha o local onde salvar e clique em OK.
Copiar aqui




Este "site", destinado prioritariamente aos alunos de Fátima Conti,
está disponível sob FDL (Free Documentation Licence),
pretende auxiliar quem se interessa por Bioestatística,
estando em permanente construção.
Sugestões e comentários são bem vindos.
Se desejar colaborar clique aqui. Agradeço antecipadamente.



Deseja enviar essa página?


Se você usa um programa de correio eletrônico devidamente configurado para
um e-mail pop3, clique em "Enviar página" (abaixo) para abrir o programa.
Preencha o endereço do destinatário da mensagem.
E pode acrescentar o que quiser.
(Se não der certo, clique aqui para saber mais).

Enviar página


Se você usa webmail copie o endereço abaixo

http://www.ufpa.br/dicas/biome/biopro.htm
Acesse a página do seu provedor. Abra uma nova mensagem.
Cole o endereço no campo de texto.
Preencha o endereço do destinatário.
E também pode acrescentar o que quiser.

Última alteração: 4 dez 2012