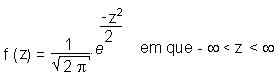Biometria
Biometria
Para
visualizar corretamente configurar a tela para 1024 x 768 pixels
Algumas distribuições
| Binomial
| Normal
| Poisson
|
A distribuição Binomial
É uma das
distribuições
mais comuns em Estatística. Uma variável
aleatória tem
distribuição binomial quando o experimento ao
qual está relacionada apresenta apenas 2 resultados
(sucesso ou fracasso). Exemplo:
Lançamento de uma moeda.
Deriva de um processo conhecido
como teste de Bernoulli, em que cada tentativa tem duas possibilidades
excludentes
de ocorrência (sucesso e fracasso).
O Processo de Bernoulli
Uma seqüência de testes
de Bernoulli forma um Processo de Bernoulli, se obedecer as seguintes
condições:
a.
Cada tentativa admite dois resultados, que são
mutuamente
excludentes. Denomina-se, arbitrariamente, um dos resultados
de sucesso e o outro de
fracasso. Chama-se a probabilidade de sucesso de
"p". Ela permanece
constante
em todas as tentativas. Já a probabilidade de fracasso,
(1
-
p), é denominada "q";
b.
n provas independentes e do mesmo tipo
são realizadas;
c.
O resultado de uma tentativa não é
afetado pelos
resultados das outras tentativas, ou seja, as tentativas são
independentes.
Propriedades
1. f
(x) >=
0, para todo x pertencente a R
2. 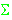 f
(x) = 1
f
(x) = 1 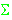 n
Cx .p x.q (n-x)
(em que C
= número de combinações).
n
Cx .p x.q (n-x)
(em que C
= número de combinações).
Equivale
à
expansão
do binômio:
(p + q)n =
1.p0.qn
+ _. p1.qn-1
+ ... + _. pn-1.q1
+ 1.
pn.q0
em que os coeficientes podem ser obtidos
pelo Triângulo
de Pascal.
3. São
conhecidos os
parâmetros
da distribuição binomial (n e p), portanto,
Média
da população =  |
 p
= n.p usando o dado de um dos
acontecimentos ou p
= n.p usando o dado de um dos
acontecimentos ou
 q
= n.q usando o dado do outro
acontecimento q
= n.q usando o dado do outro
acontecimento |
Variância
da população
= 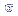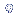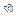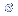 2 2 |
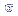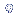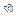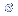 2
= n.p.(1 - p) = n.p.q 2
= n.p.(1 - p) = n.p.q |
Desvio
padrão da
população = 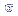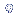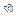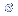 |
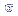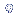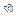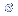 = raiz
n.p.q = raiz
n.p.q |
A distribuição de Poisson
Esta distribuição
descreve
eventos raros, em que se faz um enorme número de tentativas
e
aplica-se
à situação em que o evento (ou
entidade) de
interesse
está homogeneamente distribuído na
população.
Se x for a ocorrência de algum
evento aleatório em um intervalo de tempo ou
espaço (ou
algum
volume de matéria), a probabilidade de ocorrência
de x
é:
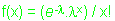 |
.
....x = 1, 2, 3, ... |
em que:
 =
parâmetro de distribuição, é
a média
de ocorrência de x
=
parâmetro de distribuição, é
a média
de ocorrência de x
e = número de Euler
( 2,71828182846... )
O Processo de Poisson
a.
A ocorrência de um evento em um intervalo de
espaço ou de
tempo não tem qualquer efeito sobre a probabilidade de
ocorrência
de um segundo evento, ou seja, a ocorrência dos eventos
é
independente;
b.
Um número infinito de ocorrências de um evento
devem ser
possíveis
no intervalo;
c.
A probabilidade de uma única ocorrência do evento
em um
dado intervalo é proporcional ao tamanho desse intervalo;
d.
Em uma porção infinitesimal do intervalo, a
probabilidade
de mais de uma ocorrência do evento é
desprezível.
 Na distribuição de
Poisson
a média e a variância são iguais
a
Na distribuição de
Poisson
a média e a variância são iguais
a  ,
que representa a taxa com que eventos são observados.
,
que representa a taxa com que eventos são observados.
Quando um se faz um grande
número
de observações, e quando o evento tem uma pequena
probabilidade
de ocorrer, o número total de eventos tem
distribuição
aproximadamente Poisson cuja taxa de ocorrência é
dada por:
 =
np
=
np
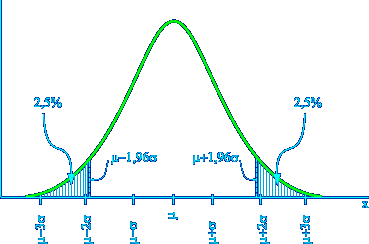
A distribuição Normal
O
gráfico que representa a curva normal tem forma
de sino, ou seja, é unimodal, e o seu valor de
máxima
freqüência
(moda) coincide com o valor da média e da mediana.
em que Média da
população
=  e
Desvio padrão da população
=
e
Desvio padrão da população
= 
A equação dessa curva é dada por:
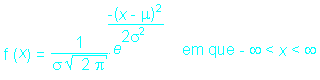
Características
a. A
distribuição
é simétrica em relação
à
média.
b. Os valores de
média,
moda e mediana são iguais.
c. A área total sob
a curva é igual a 1 (100%), com exatos 50%
distribuídos
à
esquerda e 50% à direita da média
d. A área
sob
a curva normal
|
Sub-área da curva
|
| População |
Amostra |
Valor |
 ±
1 ±
1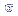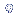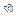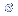 |
 ±
1s ±
1s |
68,26
% |
 ±
2 ±
2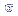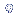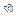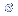 |
 ±
2s ±
2s |
95,44
% |
 ±
3 ±
3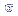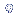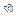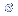 |
 ±
3s ±
3s |
99,74
% |
e. A
distribuição
normal é completamente determinada pelos
parâmetros
 Média
da população =
Média
da população =  e Desvio
padrão da
população
=
e Desvio
padrão da
população
= 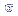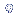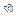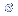
Distribuição Normal Padrão
É caracterizada pela
média
(  ) igual a zero e desvio padrão (
s)
igual a 1.
) igual a zero e desvio padrão (
s)
igual a 1.
Se x tem
distribuição
normal com média e variância
s2,
então z = (
x -  ) / s
) / s
A equação
dessa
curva é:
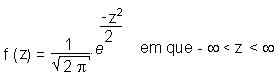

|
Copie
esse texto em formato
pdf
clicando no link ao lado com o botão direito do mouse.
Depois, clique em"Salvar destino como" (ou algo
semelhante )
Escolha o local onde salvar e clique em OK. |
Copiar aqui
|



Este "site", destinado
prioritariamente
aos alunos de Fátima Conti,
está disponível sob FDL (Free
Documentation Licence),
pretende auxiliar quem se interessa por Bioestatística,
estando em permanente
construção.
Sugestões e
comentários
são bem vindos.
Se desejar colaborar
clique
aqui.
Agradeço
antecipadamente.
Deseja enviar
essa página?
Se você usa um
programa
de correio eletrônico devidamente configurado para
um e-mail
pop3, clique em "Enviar página" (abaixo) para
abrir o
programa.
Preencha o endereço
do destinatário da mensagem.
E pode acrescentar o que quiser.
(Se não der certo,
clique aqui
para
saber mais).
Enviar
página

Se você usa webmail
copie o endereço abaixo
http://www.cultura.ufpa.br/dicas/biome/biodist.htm
Acesse a página do seu provedor. Abra uma nova mensagem.
Cole o endereço no campo de texto.
Preencha o endereço do destinatário.
E também pode acrescentar o que quiser.
Última
alteração: 10 out 2010

 Biometria
Biometria
 Biometria
Biometria![]() f
(x) = 1
f
(x) = 1 ![]() n
Cx .p x.q (n-x)
(em que C
= número de combinações).
n
Cx .p x.q (n-x)
(em que C
= número de combinações). ![]() =
parâmetro de distribuição, é
a média
de ocorrência de x
=
parâmetro de distribuição, é
a média
de ocorrência de x
 Na distribuição de
Poisson
a média e a variância são iguais
a
Na distribuição de
Poisson
a média e a variância são iguais
a  ,
que representa a taxa com que eventos são observados.
,
que representa a taxa com que eventos são observados.![]() =
np
=
np
 e
Desvio padrão da população
=
e
Desvio padrão da população
= ![]()
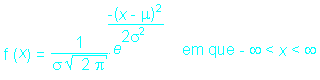
 ±
2s
±
2s Média
da população =
Média
da população = ![]() e Desvio
padrão da
população
=
e Desvio
padrão da
população
= ![]()

![]() ) / s
) / s