c
Biometria - EDAP
Para visualizar corretamente configurar a tela para 1024 x 768 pixels


Binômio de Newton e Triângulo de Pascal

(Leitura complementar ao capítulo2)


Sumário:

Binômio de Newton
Coeficientes binomiais
Herança Quantitativa ou poligênica
Triângulo de Pascal


Triângulo de Pascal

Blaise Pascal (Clermont-Ferrand, Puy-de-Dôme, 19 de Junho de 1623 - Paris, 19 de Agosto de 1662) foi um prodígio matemático.

Em torno de 1650 escreveu o "Traité du Triangle Arithmétique" publicado em 1665 e, juntamente com Pierre Fermat, estabeleceu os fundamentos da teoria da probabilidade.

Embora não tenha sido o primeiro a trabalhar com o triângulo, este tornou-se conhecido como "triângulo de Pascal" devido ao desenvolvimento e aplicações que Pascal fez de muitas de suas propriedades.

Construído do modo como se vê a seguir, e denominando-se as linhas de n = 1, 2, ... e as colunas de r = 0, 1, 2, ...

Cada entrada C(n,r) é a soma do número acima com o da sua esquerda (também acima) de cada número.

Exemplo:
O número 2, na posição C(2, 1) é obtido pela soma de 1 (número acima dele) + 1 (número à esquerda, também acima).
O número 10, na posição C(5, 2) é obtido pela soma de 6 (número acima dele) + 4 (número à esquerda, também acima)

n, r r = 0 r = 1 r = 2 r = 3 r = 4 r = 5 r = 6
n = 0 1 . . .. . . .
n = 1 1 1 . . . . .
n = 2 1 2 1 . . . .
n = 3 1 3 3 1 . . .
n = 4 1 4 6 4 1 . .
n = 5 1 5 10 10 5 1 .
n = 6 1 6 15 20 15 6 1

e prossegue-se até atingir os valores de n e r desejados.

Exercício

Complete: O número 20, na posição C( __, __ ), é obtido pela soma de __ + __.


Coeficientes binomiais

Uma das aplicações que Pascal fazia do seu triângulo era a determinação dos coeficientes binomiais quando se faz a expansão do binômio de Newton, sendo que eles correspondem aos números C(n,r).

Por exemplo, a fórmula
(p +q)2 = 1p2 + 2pq + 1q2

tem os coeficientes 1, 2 e 1, que estão, precisamente, na linha n = 2 no triângulo.

Já, se alguém desejar a expansão de (p +q)3 deverá tomar a linha n = 3 no triângulo.

(p +q)3 = 1p3q0 + 3p2q1 + 3p1q2 + 1p0q3

É importante lembrar que os coeficientes também podem ser obtidos diretamente pela fórmula:

C(n, r) = n! / r!.(n - r)!
Resumindo:

no. genes coeficientes no. de combinações
0 1 1
1 1 1 2
2 1 2 1 4
3 1 3 3 1 8
4 1 4 6 4 1 16
5 1 5 10 10 5 1 32
6 1 6 15 20 15 6 1 64
7 1 7 21 35 35 21 7 1 128
8 1 8 28 56 70 56 28 8 1 256 e continua...


Binômio de Newton


Isaac Newton, físico e matemático inglês (1642 - 1727) deu enorme contribuição à Matemática, em 1687 quando escreveu "Principia Mathematica".

Aqui é importante lembrar que denomina-se Binômio de Newton, a todo binômio da forma (a + b)n, sendo n um número natural, que é chamado de ordem do binômio.

Assim, para determinar quais são as combinações possíveis quando uma distribuição possui os parâmetros p e q, faz-se a expansão do

Binômio de Newton: (p + q)n

Para expandir uma equação, pode-se seguir os passos:

1. Todos os membros terão o termo p e, também, o q. (Ou seja, deve existir o termo p.q em todos os termos).

2. No primeiro membro atribui-se ao expoente de p o valor n e ao expoente de q o valor 0. A seguir diminui-se de 1 o valor do expoente de p e aumenta-se de 1 o valor do expoente de q. Continua-se até o último membro que deve ter o valor 0 no expoente de p o valor n no expoente de q.

3. A soma dos expoentes de cada membro deve ser igual ao expoente do binômio.

Portanto, a expansão de (p + q)2 é:
(p + q)2 = __ p2q0 + __ p1q1 + __ p0q2

Lembrando que qualquer número elevado a zero é igual a 1 e que não é necessário colocar o expoente quando for igual a 1, temos:

(p + q)2 = __ p2 + __ pq + __ q2

4. Toma-se a sequência numérica obtida no triângulo referente ao número de combinações usado e distribui-se, ordenadamente.


No. Comb. Binômio
 Equação expandida
4 (p + q)2 1p2q0 + 2p1q1 + 1p0q2
8 (p + q)3 1p3q0 + 3p2q1 + 3p1q2 + 1p0q3
16 (p + q)4 1p4q0 + 4p3q1 + 6p2q2 + 4p1q3 + 1p0q4
E continua...

Assim, a expansão de (p + q)2 gera:

p2 + 2pq + q2


Para descobrir quais são os coeficientes das equações com expoentes maiores que 4 é conveniente usar o Triângulo de Pascal, como descrito acima.

Herança quantitativa (ou poligênica)

Na herança quantitativa dois ou mais pares de alelos determinam o fenótipo. Por isso é também denominada herança poligênica.

Os alelos podem ser: aditivo ou indiferente (ou não-aditivo).

Cada alelo aditivo determina o aumento da intensidade da expressão do fenótipo, não importando de qual par é esse alelo aditivo.

Os alelos não-aditivos não acrescentam nada na expressão do fenótipo.


Herança quantitativa - Identificação

Como identificar e diferenciar a herança quantitativa das demais heranças genéticas?
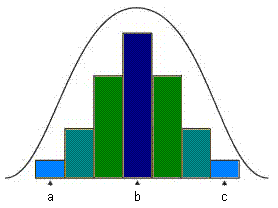
Na geração F2 há vários fenótipos para uma certa característica, com variação contínua.

Quando estão envolvidos 2 pares de genes haverá 5 fenótipos possíveis. Se forem 3 pares serão 7 fenótipos. Se forem 4 pares serão 9 fenótipos e assim por diante.

Em F2 o fenótipo apresenta variação contínua ou gradual. Exemplo: No caso da cor da pele na espécie humana, entre os extremos (branco e negro) há diversos fenótipos intermediários, os vários tipos de mulatos.

A frequência dos fenótipos se distribui em uma curva normal.

Os fenótipos dos tipos extremos (mínimos e máximos) são os observados em frequências menores, enquanto os fenótipos intermediários são encontrados em quantidades maiores. A distribuição quantitativa desses fenótipos estabelece uma curva normal e mostra a expressividade do caráter.




Expressividade do caráter
a = mínima, b = média, c = máxima

Algumas fórmulas podem ajudar a resolver problemas:

1. O número de fenótipos que podem ser encontrados depende do número de pares de alelos envolvidos, que chamamos

n = número de fenótipos = 2n + 1

2. Pode-se calcular a frequência dos fenótipos extremos
Frequência de 1 fenótipo extremo = (1/4)n

3. Pode-se calcular quanto cada gene aditivo acrescenta ao fenótipo. ( Lembrar que número de genes = 2n).

Valor do gene aditivo = (fenótipo máximo - fenótipo míimo ) / 2n

Exemplo: Cor da pele humana

No caso da cor da pele humana, considerando apenas 5 fenótipos, envolvendo dois pares de genes N e B, que teriam a mesma função, ou seja, acrescentar uma certa quantidade de melanina à pele, se efetivos (N ou B) ou não acrescentar nada, se não efetivos (n ou b).

Fenótipos Número de genes
negro 4 genes efetivos e 0 não efetivos
mulatos escuros 3 genes efetivos e 1 não efetivo
mulatos médios 2 genes efetivos e 2 não efetivos
mulatos claros 1 gene efetivo e 3 não efetivos
branco 0 genes efetivos e 4 não efetivos

Se acontecer um cruzamento entre dihíbridos, quais serão as proporções fenotípicas da descendência?


Resolução 1:

Com conhecimentos de Genética: (quais são os gametas e os tipos possíveis de filhos gerados?)


NnBb x NnBb
Gametas produzidos por ambos: NB, Nb, nB e nb
gametas NB Nb nB nb
NB NNBB NNBb NnBB NnBb
Nb NNbB NNbb NnbB Nnbb
nB nNBB nNBb nnBB nnBb
nb nNbB nNbb nnbB nnbb

Observa-se que há 16 combinações genotípicas diferentes, sendo :

1 negro 4 genes efetivos e 0 não efetivo NNBB menor frequência = 1/16 maior expressividade
4 mulatos escuros 3 genes efetivos e 1 não efetivo NNBb ou nNBB . .
6 mulatos médios 2 genes efetivos e 2 não efetivos NNbb, nnBB ou NnBb maior frequência = 6/16 média expressividade
4 mulatos claros 1 gene efetivo e 3 não efetivos Nnbb ou nnBb . .
1 branco 0 gene efetivo e 4 não efetivos nnbb menor frequência = 1/16 mínima expressividade

Ou seja, na descendência chega-se à seguinte proporção fenotípica: 1 negro : 4 mulatos escuros : 6 mulatos médios : 4 mulatos claros : 1 branco


Resolução 2:

Usando o Triângulo de Pascal:
Chama-se de p = genes efetivos = 2 (N ou B) e de q = genes não efetivos = 2 (n ou b)
Procura-se no triângulo a linha em que o número de genes é igual a 4.

no. genes coeficientes
0 1
1 1 1
2 1 2 1
3 1 3 3 1
4 1 4 6 4 1

1 negro 4 efetivos e 0 não efetivo 1 p4 q0
4 mulatos escuros 3 efetivos e 1 não efetivo 4 p3q1
6 mulatos médios 2 efetivos e 2 não efetivos 6 p2q2
4 mulatos claros 1 efetivo e 3 não efetivos 4 p1q3
1 branco 0 efetivo e 4 não efetivos 1 p0 q4

Portanto, na descendência chega-se à seguinte proporção fenotípica:

1 negro : 4 mulatos escuros : 6 mulatos médios : 4 mulatos claros : 1 branco


E a equação será:
(p + q)4 = 1 p4q0 + 4 p3q1 + 6 p2q2 + 4 p1q3 + 1 p0q4

ou seja:

(p + q)4 = p4 + 4 p3q + 6 p2q2 + 4 pq3 + q4



Exercícios

Qual é a equação que representa a expansão dos seguintes binômios:

a. (p + q)6

b. (p + q)8



Copie esse texto em formato pdf
clicando no link ao lado com o botão direito do mouse.


Depois, clique em"Salvar destino como" (ou algo semelhante )
Escolha o local onde salvar e clique em OK.
Copiar aqui



Acesse uma resolução clicando aqui



Este "site", destinado prioritariamente aos alunos de Fátima Conti,
está disponível sob FDL (Free Documentation Licence),
pretende auxiliar quem se interessa por Bioestatística,
estando em permanente construção.
Sugestões e comentários são bem vindos.
Se desejar colaborar clique aqui. Agradeço antecipadamente.



Deseja enviar essa página?


Se você usa um programa de correio eletrônico devidamente configurado para
um e-mail pop3, clique em "Enviar página" (abaixo) para abrir o programa.
Preencha o endereço do destinatário da mensagem.
E pode acrescentar o que quiser.
(Se não der certo, clique aqui para saber mais).

Enviar página


Se você usa webmail copie o endereço abaixo

http://www.cultura.ufpa.br/dicas/biome/biotri.htm
Acesse a página do seu provedor. Abra uma nova mensagem.
Cole o endereço no campo de texto.
Preencha o endereço do destinatário.
E também pode acrescentar o que quiser.


Última alteração: 1 abr 2011