
 Biometria
BiometriaPara visualizar corretamente configurar a tela para 1024 x 768 pixels

 Biometria
Biometria|
|
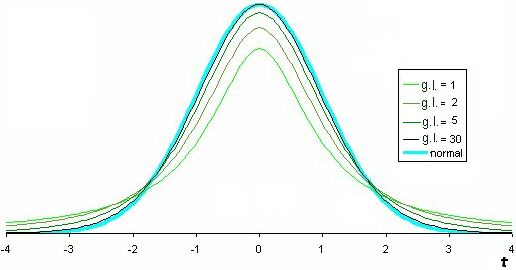
Figura: Tamanho amostral, distribuições t e normal
| Teste |
|
|
| Bicaudal |
|
|
| Monocaudal |
|
|
 d2
- [(
d2
- [( d)2
/
n] / n(n-1)
d)2
/
n] / n(n-1)
| H.
Nula: A
média dos desvios ( |
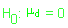 |
| H. Alternativa: A média dos desvios é diferente de zero. (Teste bicaudal) | 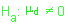 ou ou |
| H. Alternativa: A média dos desvios é maior que zero. (Teste monocaudal 1) | 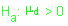 ou ou |
| H. Alternativa: A média dos desvios é menor que zero. (Teste monocaudal 2) |  |
| t
<
- tc rejeita-se a hipótese nula |
- tc | -
tc < t
< +
tc aceita-se a hipótese nula |
+ tc | t
>
+ tc rejeita-se a hipótese nula |
| Se t < tc aceita-se a hipótese nula. | tc | Se t > tc rejeita-se a hipótese nula. |
|
|
|
|
|
|
|
|
4 | 5 | -1 | 1 |
|
|
8 | 7 | 1 | 1 |
|
|
4 | 4 | 0 | 0 |
|
|
6 | 7 | -1 | 1 |
|
|
5 | 4 | 1 | 1 |
|
|
6 | 8 | -2 | 4 |
|
|
7 | 7 | 0 | 0 |
|
|
7 | 6 | 1 | 1 |
|
|
3 | 5 | -2 | 4 |
|
|
5 | 4 | 1 | 1 |
|
|
|
|
|
|
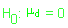
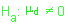 Portanto,
Portanto,
 d
/
n = -2/10 = -0,20 mm
d
/
n = -2/10 = -0,20 mm
 d2
- [(
d2
- [( d)2
/
n] / n.(n-1)
d)2
/
n] / n.(n-1)
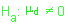 ,
o teste é bicaudal, ou seja,
interessam valores de
t
> 0 e < 0.
,
o teste é bicaudal, ou seja,
interessam valores de
t
> 0 e < 0.
|
Para facilitar os
cálculos utilize uma planilha especial:
|
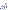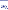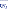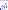 - (tc
x sd
) <
- (tc
x sd
) < |
Gêmeos
|
Técnica
N (x1)
|
Técnica
A (x2)
|
d = x1
-x2
|
d 2
|
|
1
|
54
|
55
|
-1
|
1
|
|
2
|
57
|
54
|
3
|
9
|
|
3
|
60
|
57
|
3
|
9
|
|
4
|
70
|
60
|
10
|
100
|
|
5
|
55
|
50
|
5
|
25
|
|
6
|
62
|
62
|
0
|
0
|
|
7
|
53
|
48
|
5
|
25
|
|
8
|
70
|
61
|
9
|
81
|
|
9
|
62
|
55
|
7
|
49
|
|
10
|
56
|
55
|
1
|
1
|
|
11
|
61
|
52
|
9
|
81
|
|
12
|
65
|
70
|
-5
|
25
|
|
13
|
54
|
57
|
-3
|
9
|
|
14
|
59
|
51
|
8
|
64
|
|
15
|
60
|
58
|
2
|
4
|
|
16
|
68
|
61
|
7
|
49
|
|
17
|
65
|
60
|
5
|
25
|
|
18
|
70
|
66
|
4
|
16
|
|
19
|
63
|
54
|
9
|
81
|
|
20
|
58
|
56
|
2
|
4
|
|
Total
|
1222
|
1142
|
80
|
658
|
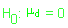
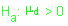
 d
/
n = 4
d
/
n = 4
 d2
- [(
d2
- [( d)2
/
n] / n(n-1)]
d)2
/
n] / n(n-1)]
| F
<
Fc As variâncias não diferem significativamente |
Fc | F
> Fc
As variâncias diferem significativamente |
| Amostra 1 | Amostra 2 |
| n1 = 100 | n2 = 131 |
| s21 = 8,00 | s22 = 7,61 |
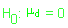
 0 ou seja,
0 ou seja, 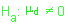 (teste bicaudal)
(teste bicaudal)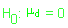
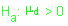 (teste monocaudal)
(teste monocaudal)
|
Para facilitar os
cálculos utilize uma planilha especial: |
| Amostra 1 | Amostra 2 |
| n1 = 10 | n2 = 20 |
| s21 = 8,10 | s22 = 2,02 |
| gl 1 = 9 | gl2 = 19 |
|
Copie
esse texto em formato
pdf Depois, clique em"Salvar destino como" (ou algo semelhante ) Escolha o local onde salvar e clique em OK. |
|



Este
"site",
destinado prioritariamente aos alunos de Fátima Conti,
está
disponível sob FDL (Free Documentation Licence),
pretende auxiliar quem se interessa por Bioestatística,
estando em permanente construção.
Sugestões
e comentários são bem vindos.
Se desejar colaborar
clique aqui.
Agradeço
antecipadamente