
 Biometria
BiometriaPara visualizar corretamente configurar a tela para 1024 x 768 pixels

 Biometria
BiometriaSumário:
Análise da variância
Dados emparelhados e análise
de variância
Etapas do teste
Modelo fatorial
Modelo hierárquico
Modelo inteiramente casualizado com n
igual
Modelo inteiramente casualizado com n
diferente
Necessidade da análise
Para se comparar
duas médias usa-se o teste t,
como foi visto aqui.
Mas, para se comparar duas médias
de várias amostras essa solução
é pouco eficiente,
pois, dependendo do número de amostras pode existir um
grande número de pares a ser analisado.
Por exemplo, em 8 amostras há:
Número de pares = [a (a - 1)] / 2 pares possíveis, ou seja: (8 x 7) / 2 = 28 pares
Ou seja, seria necessário fazer 28 testes e depois analisar resultados que poderiam divergir.
Para resolver esse tipo de problema, Fisher, em 1924,
criou a análise de variância
para comparar
simultaneamente
amostras de variáveis contínuas com
distribuição
normal e cujas variâncias não diferem
significativamente entre si, ou seja, que podem ser consideradas como
estimativas da
variância
populacional s2.
 =
= ![]()
![]() x
/ a.n =
x
/ a.n = ![]() x
/ N =
x
/ N = ![]()
 / a em que N = a.n
/ a em que N = a.n
Como a soma de quadrados
em relação às amostras reunidas
poderá ser
apresentada sob forma de:
SQT = ![]()
![]() (x -
(x - ![]() )2 =
)2 = ![]() (x
-
(x
- ![]() )2
] / (N -1)
)2
] / (N -1)
Considerando-se que
tal soma de quadrados tem N - 1 GL, a variância total pode
ser descrita como:
s2T
=
[ ![]()
![]() (x -
(x - ![]() )2] / N -1 =
)2] / N -1 = ![]() (x
-
(x
- ![]() )2 / (N -1)
)2 / (N -1)
SQE
= n ![]() (x
-
(x
- ![]() 2)
e s2E
= n [
2)
e s2E
= n [ ![]() (x
-
(x
- ![]() )2]
/ (a -1)
)2]
/ (a -1)
 ,
estabelece-se as seguintes hipóteses:
,
estabelece-se as seguintes hipóteses: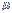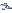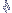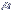 ,
pois não há diferenças significativas
entre elas
,
pois não há diferenças significativas
entre elas
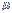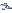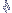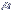 ,
pois são diferentes entre si.
,
pois são diferentes entre si.|
Se F for menor que Fc pode-se aceitar H0 e rejeitar Ha, ou seja: conclui-se que as médias das a amostras não diferem significativamente entre si e as amostras pertencem à mesma população. |
A análise de variância tem
basicamente 3 passos:
| n iguais |  =
2,3026 . (n -1) . (a log =
2,3026 . (n -1) . (a log 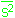 -
-  log s2) log s2) |
GL = a - 1 |
| n diferentes |  =
2,3026 . log =
2,3026 . log 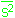 .
.  (n-1) - [
(n-1) - [ (n-1).log s2]
(n-1).log s2] |
GL = a - 1 |
Notar que 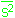 = variância média.
= variância média.
| Fonte de Variação |
|
|
|
|
F(c,
GLE, GLD) Tabela 5% |
| Verificar
o valor de F(c, GLE, GLD)
Se F < Fc
admite-se que: |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1. Quatro amostras
de
escolares brasileiros foram inoculadas com tuberculina, tendo a leitura
da reação de Mantoux (em mm) sido feita
após 48 hs
da inoculação. Obteve-se os resultados abaixo.
Por
à
prova a hipótese de que as amostras podem ser consideradas
como
pertencentes a uma mesma população.
|
Valores
|
Amostra
1
|
Amostra
2
|
Amostra
3
|
Amostra
4
|
TOTAL
|
|
|
|
63
|
60
|
63
|
62
|
|
248
|
 |
6,3
|
6,0
|
6,3
|
6,2
|
|
6,20
|
|
|
431
|
388
|
433
|
428
|
|
1.680
|
|
(
|
396,9
|
360,0
|
396,9
|
384,4
|
[
|
1.538,2
|
|
SQ
|
34,1
|
28,0
|
36,1
|
43,6
|
|
141,8
|
|
s2
|
3,79
|
3,11
|
4,01
|
4,84
|
s2
|
3,94
|
|
n
|
10
|
10
|
10
|
10
|
N
|
40
|
| Amostra | s2 | log s2 |
| 1 | 3,79 | 0,579 |
| 2 | 3,11 | 0,493 |
| 3 | 4,01 | 0,603 |
| 4 | 4,84 | 0,685 |
| Total | 15,75 | 2,360 |
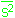 =
15,75 / 4 = 3,94
=
15,75 / 4 = 3,94
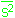 =
0,595
=
0,595![]() =
2,3026 . (n -1). (a log
=
2,3026 . (n -1). (a log 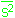 -
-![]() log
s2)
log
s2)
![]() =
2,3026 . 9. (4 . 0,595 - 2,360)
=
2,3026 . 9. (4 . 0,595 - 2,360)
![]() =
2,3026 . 9. 0,020
=
2,3026 . 9. 0,020
Portanto, ![]() = 0,414.
= 0,414.
Como G.L. =
3, ![]() = 7,815 e 0,90 < P < 0,95.
= 7,815 e 0,90 < P < 0,95.
(Para
verificar a tabela
de ![]() ,
clique
aqui).
,
clique
aqui).
Como ![]() obtido
é menor que
obtido
é menor que ![]() admite-se que as variâncias são
homogêneas.
admite-se que as variâncias são
homogêneas.
E pode-se continuar a análise.
SQT = ![]()
![]() x2
- C = 1680 -1537,6 = 142,4
x2
- C = 1680 -1537,6 = 142,4
SQE = ![]() (
(![]() x
)2 / n -
C = 1538,2 - 1537,6 = 0,6
x
)2 / n -
C = 1538,2 - 1537,6 = 0,6
| Fonte de Variação |
|
|
|
|
F(c, GLE, GLD) Tabela F, 5% |
| Verificar
o valor de F(c, GLE, GLD)
Se F < Fc
admite-se que: |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Portanto, análise
da variância aplicada aos dados acima:
| Fonte de Variação |
|
|
|
|
F(c, GLE, GLD) |
| Entre |
|
|
|
|
|
| Dentro |
|
|
|
|
|
| Total |
|
|
(Para verificar a tabela de F (5%), clique
aqui).
Conclui-se que, como F ( 0,05 )
é
menor que Fc ( 2,84 ), as amostras
pertencem
à
mesma população.
|
Análise de Variância - Modelo inteiramente casualizado Copie a planilha comprimida em formato livre ods Aba "n iguais" |
2. A
concentração
sérica de albumina foi medida em g% em 4 amostras de
hansenianos,
obtendo-se os resultados abaixo. Por à prova a
hipótese
de que as amostras podem ser consideradas como pertencentes a uma mesma
população.
|
Valores
|
Amostra
1
|
Amostra
2
|
Amostra
3
|
Amostra
4
|
TOTAL
|
|
|
|
35,61
|
29,35
|
44,71
|
38,41
|
|
148,08
|
|
|
3,56
|
3,67
|
3,73
|
4,27
|
|
3,80
|
|
|
130,83
|
109,54
|
170,80
|
166,39
|
|
577,56
|
|
(
|
126,81
|
107,68
|
166,58
|
163,93
|
|
565
|
|
SQ
|
4,02
|
1,86
|
4,22
|
2,46
|
|
12,56
|
|
s2
|
0,45
|
0,27
|
0,38
|
0,30
|
s2
|
0,33
|
|
n
|
10
|
8
|
12
|
9
|
N
|
39
|
| Amostra |
SQ
|
n -
1
|
s2
|
log
s2
|
(n-1)log
s2
|
| 1 |
4,02
|
9
|
0,45
|
-0,347
|
- 3,123
|
| 2 |
1,86
|
7
|
0,27
|
-0,569
|
- 3,983
|
| 3 |
4,22
|
11
|
0,38
|
-0,420
|
- 4,620
|
| 4 |
2,46
|
8
|
0,30
|
-0,523
|
- 4,184
|
| Total |
12,56
|
35
|
-15,910
|
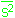 =
=
Calcula-se o
logarítmo
da variância média
log 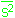 =
-0,445
=
-0,445
Substitui-se os
valores
na fórmula:
![]() =
2,3026 . [log
=
2,3026 . [log ![]() 2.
2.![]() (n
-1) -
(n
-1) - ![]() (n-1).log
s2]
(n-1).log
s2]
= 2,3026 . ( -0,445 x 35 ) - (- 15,910)
= 2,3026 . [-15,575 - - 15,910] = 2,3026 . 0,335
Portanto, ![]() =
0,717.
=
0,717.
Como G.L. =
3, ![]() = 7,815 e 0,80 < P <
0,90
= 7,815 e 0,80 < P <
0,90
Como ![]() obtido
é menor que
obtido
é menor que ![]() admite-se que as variâncias são
homogêneas.
admite-se que as variâncias são
homogêneas.
SQT = ![]()
![]() x2
- C = 577,56 - 562,25 = 15,31
x2
- C = 577,56 - 562,25 = 15,31
SQE= ![]() (
(![]() x)2
/ n - C = 565 - 562,25 = 2,75
x)2
/ n - C = 565 - 562,25 = 2,75
| Fonte de Variação |
|
|
|
|
F(c,
GLE, GLD) Tabela 5% |
| Verificar
o valor de F(c, GLE, GLD)
Se F < Fc
admite-se que: |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Análise da variância aplicada aos dados acima
| Fonte de Variação |
|
|
|
|
F(c, GLE, GLd) |
| Entre |
|
|
|
|
|
| Dentro |
|
|
|
P > 0,05 |
|
| Total |
|
|
|
Análise de Variância - Modelo inteiramente casualizado Copie a planilha comprimida em formato livre ods Aba "n diferentes" |
| grupo etário (anos) | Caucasóides | Negróides | Mongolóides |
| 10 - 20 | 4 - 3 - 5 - 8 - 2 | 5 - 6 - 9 - 5 - 6 | 7 - 4 - 6 - 4 - 4 |
| 20 - 30 | 5 - 6 - 3 - 5 - 6 | 6 - 7 - 7 - 6 - 4 | 2 - 4 - 5 - 4 - 8 |
| 30 - 40 | 6 - 6 - 6 - 4 - 3 | 4 - 7 - 5 - 7 - 6 | 3 - 8 - 4 - 3 - 5 |
| 40 - 50 | 4 - 3 - 4 - 5 - 6 | 4 - 5 - 6 - 7 - 6 | 5 - 3 - 4 - 4 - 8 |
| 50 - 60 | 5 - 6 - 3 - 6 - 6 | 7 - 8 - 9 - 8 - 9 | 4 - 3 - 5 - 5 - 6 |
| grupo racial | Valores | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | Total | |
| CAUCASÓiDES | 22 | 25 | 25 | 22 | 26 | 120;
( |
576,0 | |
| 4,4 | 5,0 | 5,0 | 5,0 | 5,2 | 4,80 | |||
| 118 | 131 | 133 | 102 | 142 | 626 | |||
| ( |
96,8 | 125,0 | 125,0 | 96,8 | 135,2 | s2 | 578,8 | |
| SQ | 5,30 | 1,50 | 2,00 | 1,30 | 1,70 | 2,08 | ||
| s2 | 5 | 5 | 5 | 5 | 5 | N | 25 | |
| NEGRÓIDES | 31 | 30 | 29 | 28 | 41 | 159;
( |
1.011,2 | |
| 6,2 | 6,0 | 5,8 | 5,6 | 8,2 | 6,36 | |||
| 203 | 186 | 175 | 162 | 339 | 1065 | |||
| ( |
192,2 | 180,0 | 168,2 | 156,8 | 336,2 | s2 | 1.033,4 | |
| SQ | 2,70 | 1,50 | 1,70 | 1,30 | 0,70 | 2,24 | ||
| s2 | 5 | 5 | 5 | 5 | 5 | N | 25 | |
| MONGOLÓIDES | 25 | 23 | 23 | 24 | 23 | 120;
( |
557,0 | |
| 5,0 | 4,6 | 4,6 | 4,8 | 4,6 | 4,72 | |||
| 133 | 125 | 123 | 130 | 111 | 622 | |||
| ( |
125,0 | 105,8 | 105,8 | 115,2 | 105,8 | s2 | 557,6 | |
| SQ | 2,00 | 4,80 | 4,30 | 3,70 | 1,30 | 2,71 | ||
| s2 | 5 | 5 | 5 | 5 | 5 | N |
25 | |
Como G.L. =
2, ![]() = 5,991
= 5,991
Como ![]() obtido
é menor que
obtido
é menor que ![]() admite-se que as variâncias são
homogêneas.
admite-se que as variâncias são
homogêneas.
SQT = ![]()
![]() x2
- C = 2.313 - 2.101,4 = 211,6
x2
- C = 2.313 - 2.101,4 = 211,6
SQE= ![]() (
(![]() x
)2 / n - C = 578,8 + 1.033,4
+ 557,6 -
2.101,4 = 68,40
x
)2 / n - C = 578,8 + 1.033,4
+ 557,6 -
2.101,4 = 68,40
Chamando o fator
raça de r e
o fator idade de i,
calcula-se a soma
dos quadrados entre os grupos raciais e entre os grupos
etários:
SQE r
=![]()
![]() (
(![]() x)2
/s.n - C = 576,0 + 1.011,2 + 557,0 -
2.101,4 = 42,80
x)2
/s.n - C = 576,0 + 1.011,2 + 557,0 -
2.101,4 = 42,80
SQE i
= ![]()
![]() (
(![]() x)2
/ a.n - C = (22 + 31 + 25)2
/ 15 + ... -
2.101,4 = 10,13
x)2
/ a.n - C = (22 + 31 + 25)2
/ 15 + ... -
2.101,4 = 10,13
SQE interação = SQE - SQEr - SQEi = 68,40 - 42,80 - 10,13 = 15,47
Para se obter os
graus de liberdade opera-se de modo semelhante, chegando-se a g.l. = 8
na SQE interação.
| Fonte de Variação | G.L. | SQ | s2 | F(GLE, GLD) |
| Entre grupos raciais | 2 | 42,80 | 21,40 | F(2,60) = 8,95; P < 0,05 |
| Entre faixas etárias | 4 | 10,13 | 2,53 | F(4,60) = 1,06; P > 0,05 |
| Interação | 8 | 15,47 | 1,93 | F(8, 60) = 0,81; P > 0,05 |
| Entre | 14 | 68,40 | 4,89 | F(14, 60) = 2,05; P < 0,05 |
| Resíduo | 60 | 143,20 | 2,39 | |
| Total | 74 | 211,60 |
|
Copie uma planilha comprimida com esse exemplo de modelo fatorial em formato livre ods |
Um pesquisador coletou
dados em 2 estados brasileiros (A e B) a respeito do peso de
recém-nascidos
de sexo masculino e que, em cada um desses estados esteve em duas
cidades:
A1, A2, B1
e B2. Portanto,
o peso pode ser classificado conforme 2 critérios: o estado
(A
ou
B) ou a cidade: A1, A2, B1
ou B2.
Os dados não podem ser reduzidos a uma tabela de
contingência,
pois as cidades não são independentes do e
estado.
Admite-se,
pois o ENCADEAMENTO DE EFEITOS, um contendo o outro, de tal modo que se
distingue uma hierarquia de efeitos.
| Estado | valores | Cidade 1 | Cidade 2 | Valores | Total |
| 5.175,000 | 4.725,000 | 9900;
( |
32.670,000 | ||
| 3,450 | 3,150 | 3,300 | |||
| a | 18.399,386 | 15.405,402 | 33.804,788 | ||
| ( |
17.853,750 | 14.883,750 | 32.737,500 | ||
| s2 | 0,364 | 0,348 | s2 | 0,378 | |
| n | 1.500 | 1.500 | 3.000 | ||
| 5.130,000 | 4.785,000 | 9915; |
32.769,075 | ||
| B | 3,420 | 3,190 | 3,305 | ||
| 18.069,250 | 15.818,780 | 33.888,030 | |||
| ( |
17.544,600 | 15.264,150 | 32.808,750 | ||
| s2 | 0,350 | 0,370 | s2 | 0,373 | |
| n | 1.500 | 1.500 | 3.000 |
a = 2 (2 amostras
= estados), s = 2 (2 subamostras =
cidades) e N
= total de indivíduos (6.000)
Como G.L. =
3, ![]() = 7,815 e 0,30 < P
<
0,50
= 7,815 e 0,30 < P
<
0,50
Como ![]() obtido
é menor que
obtido
é menor que ![]() admite-se que as variâncias são
homogêneas.
admite-se que as variâncias são
homogêneas.
SQT =![]() x2
- C = 67.692,818 - 65.439,04 = 2.253,78
x2
- C = 67.692,818 - 65.439,04 = 2.253,78
Como N - 1 = 6.000 - 1 = 5.999 g.l.
O componente que mede o efeito entre as amostras, ou seja, entre os estados, é calculado a partir de:
SQEa = [![]() (
(![]()
![]() x)
2 / sn] - C = 65.439,07 - 65.439,04 = 0,03; tendo a-1 = 2-1
= 1
g.l.
x)
2 / sn] - C = 65.439,07 - 65.439,04 = 0,03; tendo a-1 = 2-1
= 1
g.l.
O componente que mede o efeito entre as s sub-amostras dentro de cada amostra (SQes) é obtido assim:
SQE = ![]()
![]() [(
[(![]() x)2
/ n] - C = 65.546,25 - 65.439,04 = 107,21; tendo as-1 = 4-1 = 3 g.l.
x)2
/ n] - C = 65.546,25 - 65.439,04 = 107,21; tendo as-1 = 4-1 = 3 g.l.
Como SQE = SQEa + SQEs:
SQEs = 107,21 - 0,03 = 107,18; tendo a (s-1) = 2 (2-1) = 2 g.l.
A soma de quadrados do resíduo é obtida por:
SQD = SQT - SQE = SQT - SQEa - SQEs = 2.253,78 - 107,21 = 2.146,57
tendo a.s.(n -1)
= 2 . 2 . 1499 = 5.996 g.l.
| Fonte de Variação | G.L. | SQ | s2 | F(GLE, GLD) |
| Entre estados | 1 | 0,03 | 0,03 | F(1,2 = 0,0006; P > 0,05 |
| Entre cidades nos estados | 2 | 107,18 | 53,59 | F(2, i) = 148,86; P < 0,05 |
| Resíduo | 5996 | 2146,57 | 0,36 | i = infinito |
| Total | 5999 | 2253,78 |
Não
há
diferenças significativas entre as médias dos
estados A e
B, mas há diferenças entre as cidades dentro de
cada
estado.
Pode-se reanalisar
os dados levando em consideração apenas um
critério:
estado de origem, (como se o modelo fosse inteiramente casualizado).
Monta-se
a seguinte tabela:
Reanálise
da variância aplicada aos dados acima:
| Fonte de Variação | G.L. | SQ | s2 | F(GLE, GLD). |
| Entre estados | 1 | 0,03 | 0,03 | F(1, i) = 0,08; P < 0,05 |
| Dentro | 5998 | 2253,75 | 0,38 | |
| Total | 5999 | 2253,78 | i = infinito |
Como F é
menor
que Fc __________-se que haja
diferenças
significativas
entre as médias dos estados A e B.
| Tipo | Valores |
MM
|
FF
|
Total
|
Tipo | Valores | MM | FF | Total |
|
1,105
|
1,487
|
2,592
|
1,492 | 2,263 | 3,755 | ||||
| d |
0,065
|
0,087
|
0,076
|
d | 0,088 | 0,133 | 0,110 | ||
| MZ |
0,118
|
0,293
|
0,411
|
DZ | 0,203 | 0,436 | 0,639 | ||
| ( |
0,072
|
0,0130
|
0,202
|
( |
0,131 | 0,301 | 0,432 | ||
| s2 |
0,003
|
0,010
|
0,006
|
s2 | 0,005 | 0,008 | 0,007 | ||
| n |
17
|
17
|
34
|
n | 17 | 17 | 34 |
a = 2 (no. de
amostras),
s = 2 (no. de subamostras em cada amostra a) e N = total de
indivíduos
(6.000)
Como G.L. =
3, ![]() = 7,815 e 0,10 < P <
0,20
= 7,815 e 0,10 < P <
0,20
Como ![]() obtido
é menor que
obtido
é menor que ![]() admite-se que as variâncias são
homogêneas.
admite-se que as variâncias são
homogêneas.
SQT =![]() d2
- C = 1,050 - 0,592 = 0,458
d2
- C = 1,050 - 0,592 = 0,458
SQE =![]() (
(![]() d)2
/ n - C = 0,202 + 0,432 - 0,592 = 0,042
d)2
/ n - C = 0,202 + 0,432 - 0,592 = 0,042
SQEa =![]() (
(![]() d)2
/
sn - C = (2,592)2 / 34 + (3,755)2
/ 34 - 0,592 =
0,020
d)2
/
sn - C = (2,592)2 / 34 + (3,755)2
/ 34 - 0,592 =
0,020
SQEb =![]() (
(![]() d)2/an
- C = (1,105 + 1,492) 2 / 34 + (1,487 + 2,263)
2
/ 34 - 0,592 = 0,020
d)2/an
- C = (1,105 + 1,492) 2 / 34 + (1,487 + 2,263)
2
/ 34 - 0,592 = 0,020
| Fonte de Variação |
G.L.
|
SQ
|
s2
|
F(GLE,
GLD).
|
| Entre tipos de gêmeos |
1
|
0,020
|
0,0200
|
F(1,
64) = 3,08; P > 0,05
|
| Entre sexos |
1
|
0,020
|
0,0200
|
F(1,
64) = 3,08; P > 0,05
|
| Interação |
1
|
0,002
|
0,0020
|
F(3,
64) = 0,31; P > 0,05
|
| Entre |
3
|
0,042
|
0,0140
|
F(3,
64) = 2,15; P > 0,05
|
| Dentro |
64
|
0,416
|
0,0065
|
|
| Total |
67
|
0,458
|
Como F é
___
que Fc __________-se que as
diferenças intrapar em
relação
ao índice da linha T independem do tipo de gêmeos
ou do
sexo.

|
Copie
esse texto em formato
pdf Depois, clique em"Salvar destino como" (ou algo semelhante ) Escolha o local onde salvar e clique em OK. |
|
Este "site", destinado prioritariamente
aos alunos de Fátima Conti,
está disponível sob FDL (Free
Documentation Licence),
pretende auxiliar quem se interessa por Bioestatística,
estando em permanente
construção.
Sugestões e
comentários
são bem vindos.
Se desejar colaborar
clique
aqui.
Agradeço
antecipadamente.

Deseja enviar essa página?
Se você usa um
programa
de correio eletrônico devidamente configurado para
um e-mail
pop3, clique em "Enviar página" (abaixo) para
abrir o programa.
Preencha o endereço
do destinatário da mensagem.
E pode acrescentar o que quiser.
(Se não der certo,
clique aqui
para saber mais).

http://www.cultura.ufpa.br/dicas/biome/biovar.htm
Acesse a página do seu provedor. Abra uma nova mensagem.
Cole o endereço no campo de texto.
Preencha o endereço do destinatário.
E também pode acrescentar o que quiser.
Última
alteração: 7 abr 2011