
 Biometria
Biometria
Para
visualizar corretamente configurar a tela para 1024 x 768 pixels
Distribuição normal - problemas
|
A área entre
|
é
igual a |
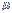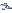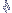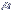 ±
1 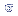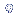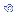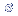 : |
68,26%
(a) |
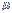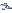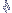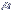 ±
2 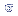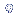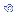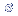 : |
95,44%
(b) |
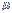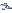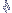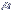 ±
3  : |
99,74%
(c) |
Exercícios - Exemplos do uso de z
1. Já
foi visto
como se chegou ao valor 68,26%. Como
se chegou aos valores (2) 95,44% e (3) 99,74%?
95,44%: - 2 < z < + 2
Qual é a área
sob a curva normal contida entre z = 0 e z
= 2 (ou z = -2) ?
Procura-se o valor 2,0 nas linhas da tabela de z
e o valor 0,00
na coluna.
O valor da
intersecção
é de 0,4772, ou seja, 47,72%.
Entretanto, lembrando que a curva normal
é simétrica, sabe-se que a
área sob a
curva contida entre z = 0 e z
= -2 também é 47,72%.
Portanto, soma-se ambas e a
área
referente
a -2 < z < 2 vale 95,44%.
99,74%: - 3 < z < + 3
Qual é a área
sob a curva normal contida entre z = 0 e z
= 3 (ou z = -3) ?
Procura-se o valor 3,0 nas linhas da tabela de z
e o valor 0,00
na
coluna. O valor da
intersecção
é de 0,4987, ou seja, 49,87%.
Sabe-se que a
área sob a
curva contida entre z = 0 e z
= -3 também é 49,87% já que a
curva
normal
é simétrica.
Portanto, soma-se ambas e a área
referente
a -3 < z < 3 vale 99,74%.
2.
Em uma população
de indivíduos adultos de sexo masculino, cuja estatura
média
é 1,70m e desvio padrão é 0,08m, qual
é o
intervalo de alturas em que 95% da população
está
compreendido?
95% = 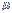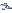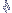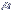 ± 1,96
± 1,96
95% = 1,70 ±
1,96
x 0,08 (sendo que 1,96 . 0,08 = 0,1568)
A maior altura será: 1,70
+ 0,1568 = 1,8568 e
a menor altura será: 1,70 - 0,1568 = 1,5432
Assim sendo, 95% da
população
tem altura entre 1,5432m e 1,8568m.
Será pouco provável
encontrar
alguém com altura superior a 1,8568m (P = 2,5%) ou abaixo de
1,5432m
(P = 2,5%).
3. Na mesma população,
qual a probabilidade de um indivíduo apresentar estatura
entre 1,60
e
1,82m?
Calcula-se dois valores de z:
zmin
= (1,60 - 1,70) / 0,08 = 1,25
zmax
= (1,82 - 1,70) / 0,08 = 1,50
Consultando a Tabela
de z, verifica-se que a área entre z
= 0 e z = -1,25 é de 39,44% e a
área
entre z = 0 e z
= 1,5 é de 43,32.%.
Portanto, a probabilidade
de
se encontrar alguém com estatura entre 1,60 e 1,82 m
é
0,3944 + 0,
4332 = 0,8276 = 82,76%
4.
Qual a probabilidade de
se encontrar 1 indivíduo com estatura menor que 1,58?
z = (1,58 - 1,70) /
0,08
= -1,5
Consultando a Tabela
de z, verifica-se que a área entre z
= 0 e z = -1,5 é 43,32.
Portanto,
a
área além de z determina a
probabilidade = 50 - 43,32 = 6,68%
5. Sabendo-se que o
índíce de
massa corpórea em
uma população de pacientes com diabetes
mellitus
obedece uma distribuição normal e tem
média = 27
kg/cm2 e desvio-padrão = 3 kg/cm2,
qual a probabilidade
de um indivíduo sorteado
nessa
população apresentar um
índíce
de massa corpórea entre 26 kg/cm2
e a µ?
Como z
= ( x - 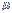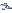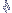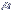 ) /
) /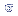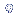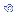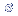 , z
= ( 26 - 27
) / 3, z
= - 0,333
, z
= ( 26 - 27
) / 3, z
= - 0,333
Consultando a Tabela
de z, verifica-se que a área entre 26 e 27
é igual a 0,1293.
Portanto, a probabilidade
de um indivíduo sorteado
nessa
população ter índice de massa
corpórea entre esses valores é 12,93%.
6. Em mulheres, a quantidade de
hemoglobina por 100ml de sangue é uma variável
aleatória com distribuição
normal de média m = 16g e desvio
padrão s
= 1g. Calcular a probabilidade de uma mulher apresentar 16 a
18g por 100ml de hemoglobina no sangue.
Como z
= ( x - 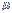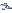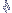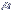 ) /
) /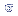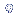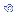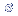 , z
= ( 18 - 16
) / 1, z = 2
, z
= ( 18 - 16
) / 1, z = 2
Consultando a Tabela
de z, verifica-se que a área entre z
= 16 e z = 18 é ,4772%. Portanto,
a
área além de z determina a
probabilidade = 47,72%.

Copie
esse
texto (comprimido) em formato pdf
clicando na extensão desejada com o botão direito
do mouse.
Depois,
clique em algo
semelhante a "Salvar destino como"
Escolha um drive
e uma pasta e clique em OK.



Este
"site",
destinado prioritariamente aos alunos de Fátima Conti,
está
disponível sob FDL (Free Documentation Licence),
pretende auxiliar quem se interessa por Bioestatística,
estando em permanente construção.
Sugestões
e comentários são bem vindos.
Se desejar colaborar
clique aqui.
Agradeço
antecipadamente
Deseja enviar
essa página?
Se
você usa um
programa de correio eletrônico devidamente configurado para
um
e-mail
pop3,
clique em "Enviar página" (abaixo) para abrir o
programa.
Preencha o endereço do destinatário da
mensagem.
E pode acrescentar o que quiser.
(Se não der
certo, clique aqui
para saber mais).
Enviar
página

Se
você usa webmail
copie o endereço
abaixo
http://www.cultura.ufpa.br/dicas/biome/bionor3.htm
Acesse
a página do seu provedor. Abra uma nova mensagem.
Cole o
endereço no campo de texto.
Preencha o endereço do
destinatário.
E também pode acrescentar o que
quiser.
Última alteração: 20 mar 2009

 Biometria
Biometria ±
1
±
1 :
: ±
2
±
2 :
: ±
3
±
3 :
: