
 Biometria
- EDAP
Biometria
- EDAPPara visualizar corretamente configurar a tela para 1024 x 768 pixels

 Biometria
- EDAP
Biometria
- EDAP
 a cada ponto da reta
corresponde exatamente um
número real,
a cada ponto da reta
corresponde exatamente um
número real,
 a cada número
real corresponde exatamente um ponto
da reta.
a cada número
real corresponde exatamente um ponto
da reta.
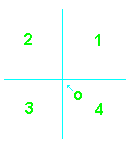
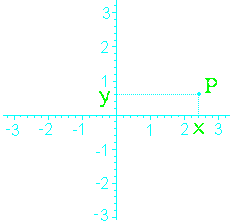
 escolher duas
retas de referência
que
não precisam
ser, necessariamente, ortogonais.
escolher duas
retas de referência
que
não precisam
ser, necessariamente, ortogonais. estabelecer o ponto de
interseção
destas retas
será a origem do sistema de
coordenadas.
estabelecer o ponto de
interseção
destas retas
será a origem do sistema de
coordenadas. estabelecer a
unidade de medida a fim
de que se possa
graduar
as duas retas e indicar claramente esta escala.
estabelecer a
unidade de medida a fim
de que se possa
graduar
as duas retas e indicar claramente esta escala.|
Copie
esse texto em formato
pdf Depois, clique em"Salvar destino como" (ou algo semelhante ) Escolha o local onde salvar e clique em OK. |
|
Este "site", destinado prioritariamente
aos alunos de Fátima Conti,
está disponível sob FDL (Free
Documentation Licence),
pretende auxiliar quem se interessa por Bioestatística,
estando em permanente
construção.
Sugestões e
comentários
são bem vindos.
Se desejar colaborar clique
aqui.
Agradeço
antecipadamente.
Deseja enviar essa página?
Se você usa um programa
de correio eletrônico devidamente configurado para
um e-mail
pop3, clique em "Enviar página" (abaixo) para
abrir o programa.
Preencha o endereço
do destinatário da mensagem.
E pode acrescentar o que quiser.
(Se não der certo,
clique aqui
para saber mais).

Se você usa webmail
copie o endereço abaixo
http://www.cultura.ufpa.br/dicas/biome/biocoorde.htm
Acesse a página do seu provedor. Abra uma nova mensagem.
Cole o endereço no campo de texto.
Preencha o endereço do destinatário.
E também pode acrescentar o que quiser.
Última
alteração: 13 mar 2011