Biometria
Para visualizar corretamente configurar a tela para 1024 x 768 pixels

Exercícios 4 - Curva normal - Resolução

4.1. Em uma amostra de indivíduos adultos de sexo masculino, cuja estatura média é 168 cm e desvio padrão é 8 cm, qual é

a. o intervalo de alturas em que 95% da população está compreendida?
95% = 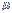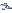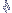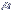± 1,96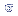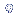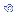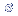
95% = 168 ± 1,96 x 8 (sendo que 1,96 . 8 = 15,68)

A maior altura será: 168 + 15,68 = 183,68 e
a menor altura será: 168 - 15,68 = 152,32

Assim sendo, 95% da população tem altura entre 152,32m e 183,68 cm.

b. a probabilidade de um indivíduo ter estatura entre 160 e 178 cm?

Calcula-se dois valores de z:
z_min = (160 - 168) / 8 = - 1,00

z_max = (178 - 168) / 8 = 1,25

Consultando a Tabela de z, verifica-se que a área entre z = 0 e z = - 1,00 é de 0,3413.
E que a área entre z = 0 e z = 1,25 é de 0,3944.

Portanto, a probabilidade de se encontrar alguém com estatura entre 160 e 178 cm é
0,3413 + 0,3944 = 0,7357 = 73,57%

c. encontrar alguém com altura superior a 183,68 cm ?
Como visto na assertiva 4.1a, 138,68 corresponde exatamente a 1,96, ou seja a 47,5% da área, portanto P = 2,5%

4.2. Uma amostra de 1000 recém-nascidos mostrou peso corporal médio igual a 3.300 g e desvio padrão igual a 700 g. Qual é:

a. o intervalo que deve conter 95% da distribuição desses pesos?

95% = ± 1,96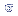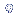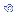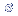
95% = 3.300 ± 1,96 x 700 (sendo que 1,96 . 700 = 1.372)

O maior peso será: 3.300 + 1.372 = 4.672 e
o menor peso será: 3.300 - 1.372 = 1.928 e

Assim sendo, 95% dos bebês têm peso entre 1,928 kg e 4,672 kg.

b. a probabilidade de um bebê ter peso igual ou superior a 2.500 g?

Calcula-se o valor de z:
z = (2500 - 3300) / 700 = - 1,14

c. encontrar um bebê com peso inferior a 1.928g?
Como visto na assertiva 4.2a, 1.928g corresponde exatamente a -1,96, ou seja a -47,5% da área, portanto P = 2,5%

d. E com peso entre 2.600 e 3.510g?

Calcula-se dois valores de z:

z_min = (2600 - 3300) / 700 = - 1,00
z_max = (3510 - 3300) / 700 = 0,30

Consultando a Tabela de z, verifica-se que a área entre z = 0 e z = -1,00 é de 0,3413 e a área entre z = 0 e z = 0,30 é de 0,1179.

Portanto, a probabilidade de um bebê ter peso entre 2.600 e 3.510g é

0,3413 + 0,1179 = 0,4592 = 45,92%

4.3. Qual a probabilidade de z pertencer à cada uma das áreas coloridas?

a. P_z (z > 2) = 0,4772
P_total ( 0 < z < + i ) = 0,5000 em que i = infinito
P_total - P_z = 0,0228 = 2,28%

b. P_z (-1 < z < 0) = - 0,3413 = 34,13%

c. P_{z min} ( -2 < z < 0) = - 0,4772
( o sinal existe para lembrar que a área se situa à esquerda da curva).
P_{z max} ( 0 < z < 1 ) = 0,3413
Portanto, P_{z min} ( -2 < z < 1 ) = 0,8185 = 81,85%

4.4. Sabe-se que a variável X tem distribuição normal, com os seguintes parâmetros: média = 30 e variância = 16.
Qual é a probabilidade de encontrarmos X > 40?

Se variância = 16, o desvio padrão (= raiz 16) = 4. Como z = ( x - ) / z = ( 40 - 30 ) /raiz 16) = 10 / 4 = 2,5 Verificando na tabela de z: Ptotal ( 0 < z < + i ) = 0,5000 em que i= infinito Pz ( 0 < z < 2,5 ) = 0,4938 Ptotal - Pz = 0,0062. Portanto, P = 0,62%

4.5. Sabe-se que a variável X tem distribuição normal, com os seguintes parâmetros: média = 60 e variância = V. Se P (X > 70) = 0,0475, qual é o valor de V?

Se a probabilidade correspondente à metade direita da curva normal é 0,5000, a probabilidade da região entre = 0 e o ponto 0,0475 é 0,5000 - 0,0475 ou seja, 0,4525 Localizando a probabilidade 0,4525 na tabela de z, encontra-se z = 1,67 Como z = ( x - ) / 1,67 = ( 70 - 60 ) /= 10 / 1,67 = = 5,988 Como variância = 2 = 35,8561

4.6. Sabe-se que a variável X tem distribuição normal, com os seguintes parâmetros: média = M e variância = 9.
Se P ( X > 28 ) = 0,1587, qual é o valor de M?

Como z = ( x - ) / então z = ( 28 - M ) / (raiz 9) = (28 - M) / 3 Como Ptotal ( M < z < + i ) = 0,5000 em que i = infinito Pz ( 0 < z < 2,5 ) = 0,1587 Portanto, P ( M <z < + 28 ) = 0,3413 Verificando na tabela de z, obtém-se z = 1,00. Então, z = ( 28 - M ) / 3 ...... 1 = ( 28 - M ) / 3 3 = 28 - M ...... ..... -25 = - M ou seja, M = 25

4.7. Considerando-se os dados do exercício anterior, z poderia ser -1?

Como z = ( x - ) / -1= ( 28 - M ) / 3 -3 = 28 - M -3 -28 = -M M = 31 A área seria 0,3413 - 0,5000 = 0,8413 Este valor não coincide com 0,1587 dado no enunciado, portanto não se pode aceitar -1 como valor de z.

4.8. Suponha que os dados abaixo referem-se a altura em cm de uma amostra de 100 universitários de sexo masculino. Agrupe-os com considerando i = 4. Depois, para os dados tabelados:

a. Calcular a média
b. Calcular o desvio padrão

Mínimo	Máximo	x	f	fx	fx2
148	152	150	0	0,00	0
152	156	154	2	308,00	47432
156	160	158	6	948,00	149784
160	164	162	5	810,00	131220
164	168	166	10	1660,00	275560
168	172	170	16	2720,00	462400
172	176	174	23	4002,00	696348
176	180	178	13	2314,00	411892
180	184	182	17	3094,00	563108
184	188	186	3	558,00	103788
188	192	190	4	760,00	144400
192	196	194	1	194,00	37636
.	.	.	100	17368,00	3023568,00
.	.	.	f = N	fx	fx2

a. Média =	fx / n =	173,6800
b. Variância = s2 =	fx2 - [(fx)2 / N]} / (N - 1)	71,6541
Desvio padrão = s =	raiz s2	raiz 71,6541 = 8,4649

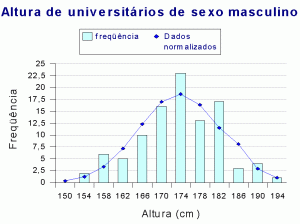
c. Traçar um gráfico em colunas da distribuição d. Sobrepor ao gráfico uma curva normal.

n =	100	M =	173,6800	s =	8,4649	n/s =	11,8135
.	.	.	.	z=	.	.	100.(yn/s)/
Min	Max	x	x - M	(X-M)/s	y	y.n/s	/ (yn/s)
148	152	150	-23,6800	-2,80	0,0079	0,0933	0,3685
152	156	154	-19,6800	-2,32	0,0270	0,3190	1,2596
156	160	158	-15,6800	-1,85	0,0721	0,8518	3,3635
160	164	162	-11,6800	-1,38	0,1539	1,8181	7,1795
164	168	166	-7,6800	-0,91	0,2637	3,1152	12,3017
168	172	170	-3,6800	-0,43	0,3637	4,2966	16,9668
172	176	174	0,3200	0,04	0,3986	4,7089	18,5949
176	180	178	4,3200	0,51	0,3503	4,1383	16,3417
180	184	182	8,3200	0,98	0,2468	2,9156	11,5133
184	188	186	12,3200	1,46	0,1740	2,0556	8,1172
188	192	190	16,3200	1,93	0,0632	0,7466	2,9483
192	196	194	20,3200	2,40	0,0224	0,2646	1,0450
.	.	.	.	.	Totais	25,3235	100,0000

4.9. Considere as 3 amostras tabeladas abaixo. Responda para cada uma delas:

a. É simétrica? b. É mesocúrtica? (C = Centro de classe)

1: Altura em 100 universitários de sexo masculino

2: Distribuição da distância inter-pupilar em 300 homens.

3: Distribuição da atividade da NADH redutase de metemoglobina em 137 homens.

1	.	.	2	.	.	3	.
C	f		C	f		C	f
.	.	.	.	.	..	.	.
150	2	.	55	1	.	16	1
153	2	.	56	3	.	20	0
156	4	.	57	4	.	24	2
159	5	.	58	6	.	28	1
162	7	.	59	10	.	32	4
165	11	.	60	23	.	36	6
168	13	.	61	28	.	40	12
171	18	.	62	36	.	44	14
174	13	.	63	50	.	48	15
177	13	.	64	37	.	52	20
180	4	.	65	32	.	56	19
183	3	.	66	26	.	60	14
186	3	.	67	24	.	64	8
189	1	.	68	12	.	68	8
192	1	.	69	4	.	72	7
Total	100	.	70	2	.	76	1
.	.	.	71	2	.	80	2
.	.	..	Total	300	.	84	2
.	..	...	..	..	..	88	0
.	.	.	.	.	.	92	0
.	.	.	.	.	.	96	0
.	.	.	.	.	.	100	1
.	.	.	.	.	.	Total	137

Amostra 1: Altura em 100 universitários de sexo masculino (i= 3).

Real	x	f	fx	fx²	fx³	fx4
150	-7	2	-14	98	-686	4802
153	-6	2	-12	72	-432	2592
156	-5	4	-20	100	-500	2500
159	-4	5	-20	80	-320	1280
162	-3	7	-21	63	-189	567
165	-2	11	-22	44	-88	176
168	-1	13	-13	13	-13	13
171	0	18	0	0	0	0
174	1	13	13	13	13	13
177	2	13	26	52	104	208
180	3	4	12	36	108	324
183	4	3	12	48	192	768
186	5	3	15	75	375	1875
189	6	1	6	36	216	1296
192	7	1	7	49	343	2401
.	.	100	-31	779	-877	18815
.	.	N =f	fx	fx²	fx³	fx4

m2 =	{(f X2)/ n - [(f X)2/ n2 ] } i2	m2 = 69,2451
m3 =	{ (f X3)/ n - (3 f X f X2)/ n2 ) + [ 2 (f X)3 / n3] } i3	m3 = -42,7918
m4 =	{ (f X4)/ n - [(4.f X.f X3)/ n2] + [ 6 (f X)2.(f X2)/ n3] - [3 (f X)4/ n4]} i4	m4 = 14720,8759

Simetria da distribuição

Curtose da distribuição

Se a amostra for grande pode-se usar as fórmulas simplificadas:

g2 = (m4 /m22) - 3	g2 = 0,0701
sg2 = raiz(24/n)	sg2 = 0,4899
t = g2 /sg2 ...... t = 0,1431	t crítico = 1,96 ...... 0,80 < P < 0,90

Como -1,96 < t < 1,96, o valor de g₂ não difere significativamente de zero, portanto é mesocúrtica.

Amostra 2: Tabela 13.4: Distribuição de 300 homens segundo a distância inter-pupilar (i = 1).

Real	x	f	fx	fx²	fx³	fx4
55	-8	1	-8	64	-512	4096
56	-7	3	-21	147	-1029	7203
57	-6	4	-24	144	-864	5184
58	-5	6	-30	150	-750	3750
59	-4	10	-40	160	-640	2560
60	-3	23	-69	207	-621	1863
61	-2	28	-56	112	-224	448
62	-1	36	-36	36	-36	36
63	0	50	0	0	0	0
64	1	37	37	37	37	37
65	2	32	64	128	256	512
66	3	26	78	234	702	2106
67	4	24	96	384	1536	6144
68	5	12	60	300	1500	7500
69	6	4	24	144	864	5184
70	7	2	14	98	686	4802
71	8	2	16	128	1024	8192
.	.	300	105	2473	1929	59617
.	.	N =f	fx	fx²	fx³	fx4

m2 =	{ (f X2)/ n - [( f X)2 / n2 ] } i2	m2 = 8,1208
m3 =	{ (f X3)/ n - (3 f X f X2) / n2 ) + [ 2 ( f X)3 / n3] } i3	m3 = -2,1398
m4 =	{ (f X4)/ n - [(4.f X. f X3) / n2] + [ 6 ( f X)2.( f X2) / n3] - [3 ( f X)4 / n4 ] } i 4	m4 = 195,7352

Simetria da distribuição

Como -1,96 < t < 1,96, o valor de de g₁ não difere significativamente de zero, portanto é simétrica.

Curtose da distribuição

Como -1,96 < t < 1,96, o valor de g₂ não difere significativamente de zero, portanto é mesocúrtica.

Amostra 3: Tab 11.4 - Distribuição da atividade da NADH redutase de metemoglobina em 137 homens (i=4).

Real	x	f	fx	fx²	fx³	fx4
16	-10	1	-10	100	-1000	10000
20	-9	0	0	0	0	0
24	-8	2	-16	128	-1024	8192
28	-7	1	-7	49	-343	2401
32	-6	4	-24	144	-864	5184
36	-5	6	-30	150	-750	3750
40	-4	12	-48	192	-768	3072
44	-3	14	-42	126	-378	1134
48	-2	15	-30	60	-120	240
52	-1	20	-20	20	-20	20
56	0	19	0	0	0	0
60	1	14	14	14	14	14
64	2	8	16	32	64	128
68	3	8	24	72	216	648
72	4	7	28	112	448	1792
76	5	1	5	25	125	625
80	6	2	12	72	432	2592
84	7	2	14	98	686	4802
88	8	0	0	0	0	0
92	9	0	0	0	0	0
96	10	0	0	0	0	0
100	11	1	11	121	1331	14641
.	.	137	-103	1515	-1951	59235
.	.	N =f	fx	fx²	fx³	fx4

m2 =	{ (f X2)/ n - [( f X)2 / n2 ] } i2	m2 = 167,8905
m3 =	{ (f X3)/ n - (3 f X f X2) / n2 ) + [ 2 ( f X)3 / n3] } i3	m3 = 630,4721
m4 =	{ (f X4)/ n - [(4.f X. f X3) / n2] + [ 6 ( f X)2.( f X2) / n3] - [3 ( f X)4 / n4 ] } i 4	m4 = 109079,3251

Simetria da distribuição

g1 = m3/ (raiz m23)	g1 = 0,2898
sg1 = raiz (6/n)	sg1 = 0,2093
t = g1 /sg1 ...... t = 1,3849	t crítico = 1,96 ......

Como -1,96 < t < 1,96, o valor de de g₁ não difere significativamente de zero, portanto é simétrica.

Curtose da distribuição:

Como -1,96 < t < 1,96, o valor de g₂ não difere significativamente de zero, portanto é leptocúrtica.

Copie esse texto (comprimido) como pdf
clicando na extensão desejada com o botão direito do mouse.

Depois, clique em algo semelhante a "Salvar destino como"
Escolha um drive e uma pasta e clique em OK.

Este "site", destinado prioritariamente aos alunos de Fátima Conti,
está disponível sob FDL (Free Documentation Licence),
pretende auxiliar quem se interessa por Bioestatística,
estando em permanente construção.

Sugestões e comentários são bem vindos.
Se desejar colaborar clique aqui. Agradeço antecipadamente.

Deseja enviar essa página?

Se você usa um programa de correio eletrônico devidamente configurado para
um e-mail pop3, clique em "Enviar página" (abaixo) para abrir o programa.
Preencha o endereço do destinatário da mensagem.
E pode acrescentar o que quiser.
(Se não der certo, clique aqui para saber mais).

Enviar página

Se você usa webmail copie o endereço abaixo

http://www.cultura.ufpa.br/dicas/biome/bioexe4r.htm

Acesse a página do seu provedor. Abra uma nova mensagem.
Cole o endereço no campo de texto.
Preencha o endereço do destinatário.
E também pode acrescentar o que quiser.

Última alteração: 20 mar 2009